题目内容
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y=
| k |
| x |
(3)若反比例函数y=
| k |
| x |
(4)若将△MNB放置于平面直角坐标系中:使斜边在横轴上,直角顶点B在反比例函数y=
| k |
| x |
分析:(1)设直线DE的解析式是y=kx+b,把D、E的坐标代入即可求出直线的解析式,把y=2代入即可求出M的坐标.
(2)把M的坐标代入反比例函数解析式求出即可,把x=4代入直线的解析式即可求出N的坐标.
(3)求出反比例函数的图象过B点的k值,即可求出答案.
(4)求出直角三角形MBN的斜边上的高BL,根据相似求出LN,即可求出N的坐标.
(2)把M的坐标代入反比例函数解析式求出即可,把x=4代入直线的解析式即可求出N的坐标.
(3)求出反比例函数的图象过B点的k值,即可求出答案.
(4)求出直角三角形MBN的斜边上的高BL,根据相似求出LN,即可求出N的坐标.
解答:解:(1)设直线DE的解析式是y=kx+b,
把D、E的坐标代入得:
,
解得:k=-
,b=3,
∴直线DE的解析式是:y=-
x+3,
∵矩形AOCB,B(4,2),
∴把y=2代入y=-
x+3得:x=2,
∴M的坐标是(2,2).
(2)把M(2,2)代入y=
得:k=4,
即反比例函数的解析式是y=
,
∵B(4,2),
∴把x=4代入y=-
x+3得:y=1,
∴N的坐标是(4,1),
把N的坐标代入y=
得:左边=4,右边=4,左边=右边,
即点N在反比例函数的图象上.
(3)把B(4,2)代入y=
得:k=8,
∵反比例函数y=
过M、N点,
∴若反比例函数y=
(x>0)的图象与△MNB有公共点,k的取值范围是4≤k≤8.
(4)过B作BL⊥MN于L,
在△MNB中,BM=4-2=2,BN=2-1=1,
由勾股定理得:NM=
=
,
S△MNB=
BM×BN=
MN×BL,
∴2×1=
×BL,
∴BL=
,
如图所示:
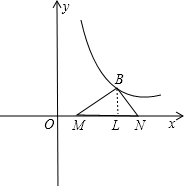
∵直角顶点B在反比例函数图象上,
∴B的纵坐标是
,代入y=
得:横坐标是2
,
∴OL=2
,
∵△MNB是直角三角形,BL⊥MN于L,
∴△BLN∽△MBN,
∴
=
,
∴
=
,
∴LN=
,
∴ON=OL+LN=2
+
=
,
∴N的坐标是(
,0).
把D、E的坐标代入得:
|
解得:k=-
| 1 |
| 2 |
∴直线DE的解析式是:y=-
| 1 |
| 2 |
∵矩形AOCB,B(4,2),
∴把y=2代入y=-
| 1 |
| 2 |
∴M的坐标是(2,2).
(2)把M(2,2)代入y=
| k |
| x |
即反比例函数的解析式是y=
| 4 |
| x |
∵B(4,2),
∴把x=4代入y=-
| 1 |
| 2 |
∴N的坐标是(4,1),
把N的坐标代入y=
| 4 |
| x |
即点N在反比例函数的图象上.
(3)把B(4,2)代入y=
| k |
| x |
∵反比例函数y=
| 4 |
| x |
∴若反比例函数y=
| k |
| x |
(4)过B作BL⊥MN于L,
在△MNB中,BM=4-2=2,BN=2-1=1,
由勾股定理得:NM=
| 22+12 |
| 5 |
S△MNB=
| 1 |
| 2 |
| 1 |
| 2 |
∴2×1=
| 5 |
∴BL=
2
| ||
| 5 |
如图所示:

∵直角顶点B在反比例函数图象上,
∴B的纵坐标是
2
| ||
| 5 |
| 4 |
| x |
| 5 |
∴OL=2
| 5 |
∵△MNB是直角三角形,BL⊥MN于L,
∴△BLN∽△MBN,
∴
| LN |
| BN |
| BL |
| MB |
∴
| LN |
| 1 |
| ||||
| 2 |
∴LN=
| ||
| 5 |
∴ON=OL+LN=2
| 5 |
| ||
| 5 |
11
| ||
| 5 |
∴N的坐标是(
11
| ||
| 5 |
点评:本题考查了用待定系数法求一次和和反比例函数的解析式,函数图象上点的坐标特征,勾股定理,三角形的面积,矩形的性质的应用,主要考查学生综合运用性质进行推理和计算的能力,有一定的难度.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: