Question

如图，已知直线l₁∥l₂，直线l₃和直线l₁、l₂交于点C和D，在C、D之间有一点P，如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD之间的关系是否发生变化.若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？

Answer 1

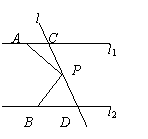
解：　若P点在C、D之间运动时，则有∠APB＝∠PAC+∠PBD.

理由是：如图4，过点P作PE∥l₁，则∠APE＝∠PAC，

又因为l₁∥l₂，所以PE∥l₂，所以∠BPE＝∠PBD，

所以∠APE+∠BPE＝∠PAC+∠PBD，即∠APB＝∠PAC+∠PBD.

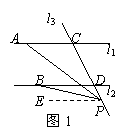
若点P在C、D两点的外侧运动时（P点与点C、D不重合），则有两种情形：

（1）如图1，有结论：∠APB＝∠PBD－∠PAC.

理由是：过点P作PE∥l₁，则∠APE＝∠PAC，

又因为l₁∥l₂，所以PE∥l₂，所以∠BPE＝∠PBD，

所以∠APB＝∠BAE+∠APE，即∠APB＝∠PBD－∠PAC.

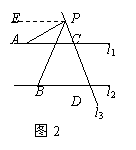
（2）如图2，有结论：∠APB＝∠PAC－∠PBD.

理由是：过点P作PE∥l₂，则∠BPE＝∠PBD，

又因为l₁∥l₂，所以PE∥l₁，所以∠APE＝∠PAC，

所以∠APB＝∠APE+∠BPE，即∠APB＝∠PAC+∠PBD.