��Ŀ����
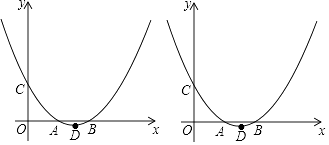
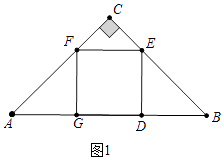
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=BC��AB=4cm���߶�AB��һ����D����1cm/s���ٶȴӵ�A�������յ�B�˶�������D��DE��AB��������AC��CB�ڵ�E����DEΪһ�ߣ���DE�����������DEFG�����˶�ʱ��Ϊx��s����0��x��4����������DEFG���ABC�ص��������Ϊy��cm2����
��1����x=sʱ����F��AC�ϣ�
��2����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��3����������DEFG������Ϊ��O��ֱ��д���˶������У�ֱ��BOƽ�֡�ABC���ʱ���Ա���x��ȡֵ��Χ��
���𰸡�
��1��![]()
��2���⣺����ͼ2�У���0��x��2ʱ���ص������ǡ�ADE��
�ߡ�C=90�㣬AC=BC��
���CAB=��AED=45�㣬
��AD=DE=x��
��y=S��ADE= ![]() x2��
x2��
����ͼ3�У���2��x�� ![]() ʱ���ص������������MNEDG��
ʱ���ص������������MNEDG��
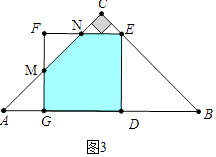
��֪FG=GD=DE=DB=4��x��MG=AG=x����4��x��=2x��4��
��FM=FG��MG=��4��x������2x��4��=8��3x=FN��
��y=S������DEFG��S��FMN=��4��x��2�� ![]() ��8��3x��2=��
��8��3x��2=�� ![]() x2+16x��16��
x2+16x��16��
�۵� ![]() ��x��4ʱ���ص�������������DEFG��
��x��4ʱ���ص�������������DEFG��
y=��4��x��2=x2��8x+16��
����������y= 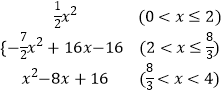
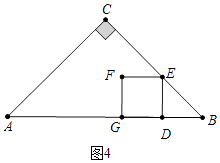
��3���⣺��ͼ5�У���2��x��4ʱ���ӳ�BO��AC��M��
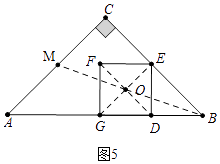
��OE=OG��EG��AC��
�� ![]() =
= ![]() =
= ![]() ��
��
��CM=AM��
��ֱ��OBƽ�֡�ABC�������
�൱2��x��4ʱ��ֱ��OBƽ�֡�ABC�����
���������⣺��1����ͼ1�У�����F��AB��ʱ����֤AG=GE=DG=DB= ![]() ��
��
���˶�ʱ��x= ![]() =
= ![]() ��
��
���Դ��� ![]() ��
��
�����㾫����������Ĺؼ�����������������ε����ʵ����֪ʶ�����յ��������ε���������ȣ���ƣ��ȱ߶ԵȽǣ����Լ��������ε����ʵ����⣬�˽��������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������Σ�