题目内容
(2014•莱芜)如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是( )

A.△CDF的周长等于AD+CD
B.FC平分∠BFD
C.AC2+BF2=4CD2
D.DE2=EF•CE
B
【解析】
试题分析:首先由正五边形的性质可得AB=BC=CD=DE=AE,BA∥CE,AD∥BC,AC∥DE,AC=AD=CE,根据有一组邻边相等的平行四边形是菱形即可证得四边形ABCF为菱形,得CF=AF,即△CDF的周长等于AD+CD,由菱形的性质和勾股定理得出AC2+BF2=4CD2,可证明△CDE∽△DFE,即可得出DE2=EF•CE.
【解析】
∵五边形ABCDE是正五边形,
∴AB=BC=CD=DE=AE,BA∥CE,AD∥BC,AC∥DE,AC=AD=CE,
∴四边形ABCF是菱形,
∴CF=AF,
∴△CDF的周长等于CF+DF+CD,
即△CDF的周长等于AD+CD,
故A选项正确;
∵四边形ABCF是菱形,
∴AC⊥BF,
设AC与BF交于点O,
由勾股定理得OB2+OC2=BC2,
∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,
∴AC2+BF2=4CD2.
故C选项正确;
由正五边形的性质得,△ADE≌△CDE,
∴∠DCE=∠EDF,
∴△CDE∽△DFE,
∴ =
= ,
,
∴DE2=EF•CE,
故D选项正确;
故选:B.


练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目


 的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )
的中点M重合,折痕分别交AB、AC于D、E,若BC=5,则线段DE的长为( )
 B.
B. C.
C. D.
D.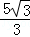

 B.
B. C.
C. D.
D.





 B.
B. C.
C. D.
D.