题目内容
12、如图，在等腰△ABC中，∠BAC=120°，DE是AC的垂直平分线，线段DE=1cm，则BD的长为（ ）分析：过A作AF∥DE交BD于F，则DE是△CAF的中位线，根据线段垂直平分线的性质，即可解答．
解答：
解：作辅助线过A做AF∥DE交BD于F，则DE是△CAF的中位线，
∴AF=2DE=2，又∵DE⊥AC，∠C=30°，∴FD=CD=2DE=2，
在△AFB中，∠1=∠B=30°，
∴BF=AF=2，∴BD=4．
故选D．
解：作辅助线过A做AF∥DE交BD于F，则DE是△CAF的中位线，∴AF=2DE=2，又∵DE⊥AC，∠C=30°，∴FD=CD=2DE=2，
在△AFB中，∠1=∠B=30°，
∴BF=AF=2，∴BD=4．
故选D．
点评：此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
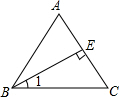如图，在等腰△ABC中，AB=AC，BE⊥AC，垂足为E，则∠1与∠A的关系式为（ ）| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
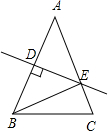如图，在等腰△ABC中，AB=AC，AB的垂直平分线DE交AB于点D，交另一腰AC于点E，若∠EBC=15°，则∠A=
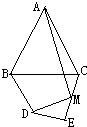24、如图，在等腰△ABC中，AB=AC，∠ABC=α，在四边形BDEC中，DB=DE，∠BDE=2α，M为CE的中点，连接AM，DM．
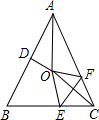（2012•丽水）如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是
如图，在等腰△ABC中，AB=AC=10cm，直线DE垂直平分AB，分别交AB、AC于D、E两点．若BC=8cm，则△BCE的周长是