题目内容
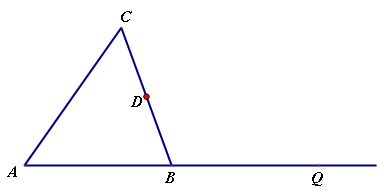
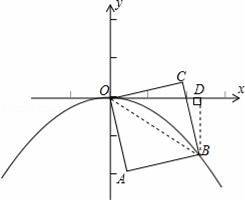
如图,四边形OABC是边长为1的正方形,OC与x轴正半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为 .


﹣
 .
.
【考点】二次函数综合题.
【专题】压轴题.
【分析】连接OB,根据正方形的对角线平分一组对角线可得∠BOC=45°,过点B作BD⊥x轴于D,然后求出∠BOD=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得BD=
 OB,再利用勾股定理列式求出OD,从而得到点B的坐标,再把点B的坐标代入抛物线解析式求解即可.
OB,再利用勾股定理列式求出OD,从而得到点B的坐标,再把点B的坐标代入抛物线解析式求解即可.
【解答】解:如图,连接OB,
∵四边形OABC是边长为1的正方形,
∴∠BOC=45°,OB=1×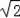
 =
=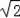
 ,
,
过点B作BD⊥x轴于D,
∵OC与x轴正半轴的夹角为15°,
∴∠BOD=45°﹣15°=30°,
∴BD=
 OB=
OB=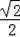
 ,
,
OD=
 =
=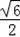
 ,
,
∴点B的坐标为(
 ,﹣
,﹣
 ),
),
∵点B在抛物线y=ax2(a<0)的图象上,
∴a(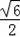
 )2=﹣
)2=﹣
 ,
,
解得a=﹣
 .
.
故答案为:﹣
 .
.

【点评】本题是二次函数综合题型,主要利用了正方形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理的应用,二次函数图象上点的坐标特征,熟记正方形性质并求出OB与x轴的夹角为30°,然后求出点B的坐标是解题的关键.

 名校课堂系列答案
名校课堂系列答案某品牌专卖店对上个月销售的男运动靯尺码统计如下, 这组统计数据中的众数是_______码.
| 码号(码) | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| 销售量(双) | 6 | 8 | 14 | 20 | 17 | 3 | 1 |
某校要从九年级(一)班和(二)班中各选取10名女同学组成礼仪队,选取的两班女生的身高如下:(单位:厘米)
 (一)班:168 167 170 165 168 166 171 168 167 170
(一)班:168 167 170 165 168 166 171 168 167 170
(二)班:165 167 169 170 165 168 170 171 168 167
(1)补充完成下面的统计分析表
| 班级 | 平均数 | 方差 | 中位数 |
| 一班 | 168 | 168 | |
| 二班 | 168 | 3.8 |
(2)请选一个合适的统计量作为选择标准,说明哪一个班能被选取.

 (代入法)
(代入法) 

 ,方差
,方差 ,样本乙的平均数
,样本乙的平均数 ,方差
,方差 ,那么两个样本波
,那么两个样本波 动的情况为( )
动的情况为( )