题目内容
4.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:| 第1天 | 第2天 | 第3天 | 第4天 | |
| 售价x(元/双) | 150 | 200 | 250 | 300 |
| 销售量y(双) | 40 | 30 | 24 | 20 |
(2)若商场计划每天的销售利润为2000元,则其单价应定为多少元?
分析 (1)根据表格中的数据可以判断x与y的函数关系,本题得以解决;
(2)根据题意可以列出相应的方程,从而可以解答本题.
解答 解:(1)由表中数据得:xy=6000,
∴$y=\frac{6000}{x}$,
∴y是x的反比例函数,
故x与y之间的函数关系式为$y=\frac{6000}{x}$;
(2)由题意得,
(x-120)•$\frac{6000}{x}$=2000,
解得,x=180;
经检验,x=180是原方程的根,
答:若商场计划每天的销售利润为2000元,则其单价应定为180元.
点评 本题考查反比例函数的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,求出相应的函数关系式和列出形应的方程.

练习册系列答案
相关题目
13.已知-6a9b4和5a4nb4是同类项,则代数式12n-10的值是( )
| A. | 17 | B. | 37 | C. | -17 | D. | 98 |
12.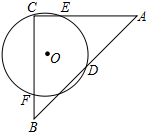 如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )
如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )
 如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )
如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为$\sqrt{3}$,AC=2+2$\sqrt{2}$,则△CEF的面积为( )| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | $2\sqrt{3}$ |
19.化简-16(x-$\frac{1}{2}$)的结果是( )
| A. | -16x-$\frac{1}{2}$ | B. | -16x+$\frac{1}{2}$ | C. | -16x-8 | D. | -16x+8 |
9.某体育场计划修建一个容积一定的长方体游泳池,若容积为V(m3),游泳池的底面积S(m2)与其深度d(m)之间的函数关系式为S=$\frac{V}{d}$(d>0),则该函数的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
13. 如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )
如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )
 如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )
如图所示,在⊙O中,OB⊥OC于点O,则∠BAC的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
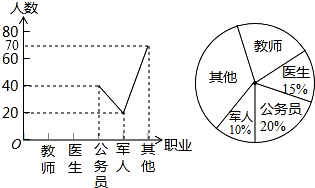 某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,并根据这组数据绘制下面两幅不完整的统计图:
某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,并根据这组数据绘制下面两幅不完整的统计图: