Question

【题目】如图，⊙O的半径为6，△ABC是⊙O的内接三角形，连接OB，OC，若∠BAC与∠BOC互补，则线段BC的长为（ ）

A.
B.3
C.
D.6

Answer 1

【答案】C
【解析】解：∵∠BAC与∠BOC互补，
∴∠BAC+∠BOC=180°，
∵∠BAC= ∠BOC，
∴∠BOC=120°，
过O作OD⊥BC，垂足为D，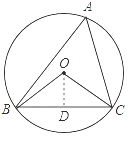

∴BD=CD，
∵OB=OC，
∴OB平分∠BOC，
∴∠DOC= ∠BOC=60°，
∴∠OCD=90°﹣60°=30°，
在Rt△DOC中，OC=6，
∴OD=3，
∴DC=3 ，
∴BC=2DC=6 ，
故答案为：C．
圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。根据定理可得∠BAC= ∠BOC，再由已知∠BAC与∠BOC互补可求∠BOC的度数，过O作OD⊥BC，垂足为D，根据垂径定理可得BD=CD，OB平分∠BOC，∠OCD的度数可求，在Rt△DOC中，用勾股定理可求DC的长，则线段BC=2DC。