题目内容
【题目】如图，在边长为4的等边
中，点D、E分别是边AC和AB的一点；
如图1，当
时，连接BD、CE，设BD与CE交于点O，
求证：
；
求
的度数；
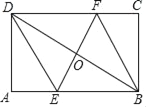
如图2，点F是边BC的中点，点D是边AC的中点，过F作
交边AB于点E，连接DE，请你利用目前所学知识试说明：
．
【答案】（1）
；
；（2）
【解析】
根据等边三角形的性质得到
，
，根据全等三角形的性质即可得到结论；
根据全等三角形的性质得到
，根据三角形的内角和即可得到结论；
延长DF到G使
，连EG，BG，根据垂直平分线的性质得到
，根据全等三角形的性质得到
，推出
是等边三角形，于是得到
，解直角三角形即可得到结论．
解：
是等边三角形，
，，
在
与
中
，
≌
，
；
由
证得≌，
，
，
；
延长DF到G使，连EG，BG，
，，
垂直平分DG，
，
在
与
中，
，
≌
，
，
又
是AC中点，
，
，
又
是BC中点，
，
，
由
，且
是等边三角形，
，
又
，
，
，
，
又
，
．
练习册系列答案
相关题目
