题目内容
 四边形ABCD与四边形A'B'C'D'位似,O为位似中心,若OA:OA'=2:3,那么SABCCD:SA'B'C'D'=________.
四边形ABCD与四边形A'B'C'D'位似,O为位似中心,若OA:OA'=2:3,那么SABCCD:SA'B'C'D'=________.
4:9
分析:四边形ABCD与四边形A'B'C'D'位似,四边形ABCD∽四边形A'B'C'D'位似,可知AD∥A′D′,△OAD∽△OA′D′,求出相似比从而求得SABCCD:SA'B'C'D'=4:9.
解答:∵四边形ABCD与四边形A'B'C'D'位似
∴四边形ABCD∽四边形A'B'C'D'位似
∴AD∥A′D′
∴△OAD∽△OA′D′
∴OA:O′A′=AD:A′D′=2:3
∴SABCCD:SA'B'C'D'=4:9.
点评:本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.
分析:四边形ABCD与四边形A'B'C'D'位似,四边形ABCD∽四边形A'B'C'D'位似,可知AD∥A′D′,△OAD∽△OA′D′,求出相似比从而求得SABCCD:SA'B'C'D'=4:9.
解答:∵四边形ABCD与四边形A'B'C'D'位似
∴四边形ABCD∽四边形A'B'C'D'位似
∴AD∥A′D′
∴△OAD∽△OA′D′
∴OA:O′A′=AD:A′D′=2:3
∴SABCCD:SA'B'C'D'=4:9.
点评:本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似比,其对应的面积比等于相似比的平方.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
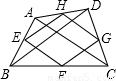
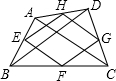 如图,已知凸四边形ABCD的两对角线BD与AC之比为k,菱形EFGH各顶点位于四边形ABCD的顺次四边之上,且EF∥AC,FG∥BD,则四边形ABCD与菱形EFGH的面积之比为
如图,已知凸四边形ABCD的两对角线BD与AC之比为k,菱形EFGH各顶点位于四边形ABCD的顺次四边之上,且EF∥AC,FG∥BD,则四边形ABCD与菱形EFGH的面积之比为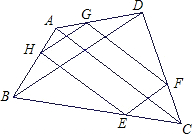 在四边形ABCD中,AC、BD是四边形ABCD的两条对角线,点E、F、G、H分别是在四边形ABCD的四边上的动点,但E、F、G、H不与A、B、C、D重合,且EF∥BD∥GH,FG∥AC∥HE.
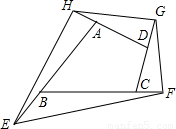
在四边形ABCD中,AC、BD是四边形ABCD的两条对角线,点E、F、G、H分别是在四边形ABCD的四边上的动点,但E、F、G、H不与A、B、C、D重合,且EF∥BD∥GH,FG∥AC∥HE. 11、如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为
11、如图,延长四边形ABCD的四边分别至E、F、G、H,使AB=nBE,BC=nCF,CD=nDG,DA=nAH(n>0),则四边形EFGH与四边形ABCD的面积之比为