Question

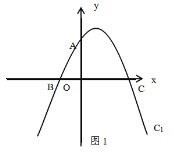
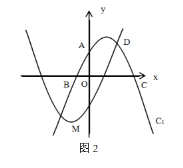
【题目】如图(1),在平面直角坐标系x Oy中,直线y=2x+4与y轴交于点A,与x轴交于点B,抛物线C1:y=x2+bx+c过A，B两点，与x轴的另一交点为点C.

(1)求抛物线C1的解析式及点C的坐标；

(2)如图(2),作抛物线C2,使得抛物线C2与C1恰好关于原点对称,C2与C1在第一象限内交于点D，连接AD，CD，请直接写出抛物线C2的解析式和点D的坐标.

(3)已知抛物线C2的顶点为M,设P为抛物线C1对称轴上一点，Q为直线y=2x+4上一点，是否存在以点M，Q，P，B为顶点的四边形为平行四边形?若存在，直接写出点P的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）y=x2+x+4，C（8，0）；

（2）y=x2+x-4，D（4，6）；

（3）（3，）或（3，）；

【解析】

（1）先求出直线y=2x+4与x轴、y轴交点坐标，待定系数法求抛物线解析式即可；

（2）根据两抛物线关于原点对称，将抛物线C1的解析式中的x和y分别换成-x和-y，整理后即为抛物线C2的解析式；再通过解方程组求点D的坐标；

（3）过B作BN∥y轴，过M作MN∥x轴与BN交于点N，分两种情形分别求点P的坐标：①BM为平行四边形的边，②BM为平行四边形的对角线．

（1）∵直线y=2x+4与y轴交于点A，与x轴交于点B，∴A（0，4），B（-2，0），

∵抛物线C1：y=-x2+bx+c过A，B两点，

∴c=4，0=-×（-2）2-2b+4，解得b=

∴抛物线C1的解析式为：y=-x2+x+4

令y=0，得-x2+x+4=0，解得x1=-2，x2=8

∴C（8，0）；

（2）∵抛物线C2与C1恰好关于原点对称，

∴抛物线C2的解析式为y=x2+x-4，

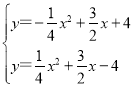解方程组得：，，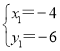

∵点D在第一象限内，

∴D（4，6）；

（3）存在．

过B作BN∥y轴，过M作MN∥x轴与BN交于点N，

∵抛物线C2的解析式为y=x2+x-4= (x+3)2-，

∴顶点M（-3，-），

∴BN=，MN=1，

抛物线C1的对称轴为：直线x=3，设P（3，m）

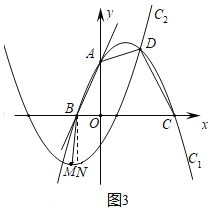
①以点M，Q，P，B为顶点的四边形为平行四边形，若MQ为对角线，则BM∥PQ，BM=PQ

∴Q（4，m+），

又∵Q为直线y=2x+4上一点，

∴m+=2×4+4，解得：m=

∴P（3，）；

②若BM为对角线，设P（3，m），Q（n，2n+4），

∵BM中点坐标为（-，）

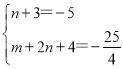∴，解得，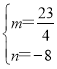

∴P（3，），

③若BQ为对角线，∵BM∥PQ，BM=PQ，∴Q（2，8），设P（3，m），

则m-=8+0，解得：m=，

∴P（3，）

综上所述，存在以点M，Q，P，B为顶点的四边形为平行四边形，点P的坐标为P（3，）或P（3，）．