题目内容
在锐角△ABC中，∠A=75°，sinC=
，则∠B= ．
【答案】分析：sinC=
，可求出∠C的值；利用内角和是180°求出∠B．
解答：解：在锐角△ABC中，
∵sinC=
，
∴∠C=60°．
∴∠B=180°-75°-60°=45°．
点评：考查了特殊角的三角函数值及三角形内角和定理．
，可求出∠C的值；利用内角和是180°求出∠B．解答：解：在锐角△ABC中，
∵sinC=
，∴∠C=60°．
∴∠B=180°-75°-60°=45°．
点评：考查了特殊角的三角函数值及三角形内角和定理．
练习册系列答案
相关题目
在锐角△ABC中，a、b、c分别表示为∠A、∠B、∠C的对边，O为其外心，则O点到三边的距离之比为（ ）
| A、a：b：c | ||||||
B、
| ||||||
| C、cosA：cosB：cosC | ||||||
| D、sinA：sinB：sinC |
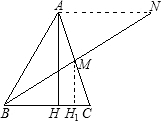在锐角△ABC中，最大的高线AH等于中线BM，求证：∠B＜60°（如图）．
如图，在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①B、E、D、C四点共圆；②AD•AC=AE•AB；③△DEF是等边三角形；④当∠ABC=45°时，BE=
（2013•南开区一模）在锐角△ABC中，∠BAC=60°，BD、CE为高，F是BC的中点，连接DE、EF、FD，则以下结论中一定正确的个数有（ ）