题目内容
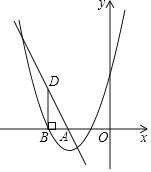
【题目】已知:直线y=ax+b与抛物线![]() 的一个交点为(0,2),同时这条直线与x轴相交于点A,且相交所成的角为45°.
的一个交点为(0,2),同时这条直线与x轴相交于点A,且相交所成的角为45°.
(1)点A的坐标为__________;
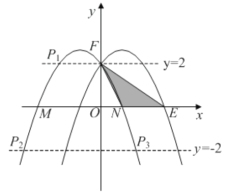
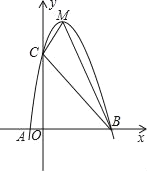
(2)若抛物线![]() 与x轴交于点M、N(点M在点N左边),将此抛物线作关于y轴对称,M的对应点为E,两抛物线相交于点F,连接NF,EF得△NEF,P是轴对称后的抛物线上的点,使得△NEP的面积与△NEF的面积相等,则P点坐标为_________.
与x轴交于点M、N(点M在点N左边),将此抛物线作关于y轴对称,M的对应点为E,两抛物线相交于点F,连接NF,EF得△NEF,P是轴对称后的抛物线上的点,使得△NEP的面积与△NEF的面积相等,则P点坐标为_________.

【答案】(-2,0)或(2,0) (2,2)或(![]() -1,-2)或(-
-1,-2)或(-![]() -1,-2)
-1,-2)
【解析】
(1)设(0,2)为点B,根据直线与y轴的交点坐标,以及与x轴的相交夹角角度,可知OB=OA=2,即可得点A的坐标;
(2)根据(1)的结论,代入直线解析式,求出a,b的值,再代入抛物线的解析式求c的值,根据抛物线与x轴有两个交点求出抛物线的解析式,根据题意作出关于y轴对称的图象,求出各个交点的坐标.设点P的坐标为(x,y),根据三角形的面积公式可知△NEP与△NEF的高相等,由此判断y的取值,将y代入抛物线的解析式即可求出点P的坐标.
解:(1)设直线与抛物线的交点(0,2)为点B,
则将点B代入直线y=ax+b,解得b=2,
且直线与x轴相交的夹角为45°,
则△AOB为等腰直角三角形,
∴OA=OB=2,
当a>0,点A的坐标为(-2,0),
当a<0,点A的坐标为(2,0),
∴点A的坐标为(-2,0)或(2,0).
(2)当a>0时,将A(-2,0),B(0,2)代入直线解析式得![]() ,解得
,解得![]() ,
,
又∵抛物线过点B(0,2),
∴ c=2,
∴抛物线的解析式为![]() ,
,
∵![]() ,
,
∴抛物线与x轴没有交点.
当a<0时,将A(2,0),B(0,2)代入直线解析式得![]() ,解得
,解得![]() ,
,
又∵抛物线过点B(0,2),
∴ c=2,
∴抛物线的解析式为![]() ,
,
∵![]() ,
,
∴抛物线与x轴有两个交点,
∴抛物线的解析式为![]() .
.
令y=0,得![]() ,解得
,解得![]() ,
,![]() ,
,
∵点M在点N左边,
∴点M的坐标为(![]() ,0),点N的坐标为(
,0),点N的坐标为(![]() ,0),
,0),
此抛物线作关于y轴对称,图象如下图所示,M的对应点为E,两抛物线相交于点F,即点F为点B,
∴点F的坐标为(0,2),点E的坐标为(![]() ,0),
,0),
∴NE=![]() -(
-(![]() )=2,OF=2,
)=2,OF=2,
∴![]() ,
,
设使得△NEP的面积与△NEF的面积相等的P点坐标为(x,y),
由三角形面积公式可知,以NE为底,要使△NEP的面积与△NEF的面积相等,则高一样,
∴![]() ,即
,即![]() .
.
当![]() 时,代入
时,代入![]() ,解得
,解得![]() ,
,![]() ,
,
∵(0,2)与点F重合,
∴点P的坐标为(﹣2,2);
当![]() 时,代入
时,代入![]() ,解得
,解得![]() ,
,![]() ,
,
∴点P的坐标为(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2),
,﹣2),
综上所述,满足条件的点P共有三个,其坐标分别为(﹣2,2)或(![]() ,﹣2)或(
,﹣2)或(![]() ,﹣2).
,﹣2).