题目内容
 如图,AB为⊙O直径,CD过OA的中点E并垂直于OA,连接CB,则∠ABC=
如图,AB为⊙O直径,CD过OA的中点E并垂直于OA,连接CB,则∠ABC=30°
30°
.分析:连接OC,由CD过OA的中点E可知AE=OE=
OC,故可得出∠EOC=30°,∠AOC=60°,根据圆周角定理即可得出结论.
| 1 |
| 2 |
解答: 解:连接OC,
解:连接OC,
∵CD过OA的中点E并垂直于OA,
∴AE=OE=
OC,
∴∠EOC=30°,∠AOC=60°,
∴∠ABC=
∠AOC=
×60°=30°.
故答案为:30°.
 解:连接OC,
解:连接OC,∵CD过OA的中点E并垂直于OA,
∴AE=OE=
| 1 |
| 2 |
∴∠EOC=30°,∠AOC=60°,
∴∠ABC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:30°.
点评:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
 6、如图,AB为直径,∠BED=40°,则∠ACD=( )
6、如图,AB为直径,∠BED=40°,则∠ACD=( )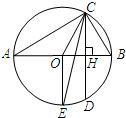 如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
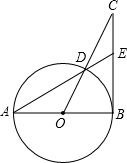 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=25°,求∠A的度数. 如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数.
如图,AB为⊙O直径,BC切⊙O于B,CO交⊙O交于D,AD的延长线交BC于E,若∠C=20°,求∠A的度数. 如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为
如图,AB为⊙O直径,BC与半径OD垂直于点C,∠B=28°,则∠A的度数为