Question

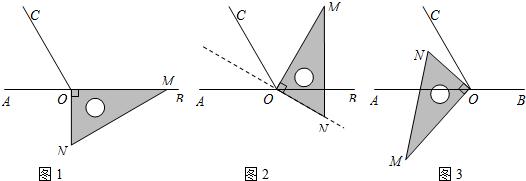
如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC：∠BOC=2：1，将一直角三角板的直角顶点放在点O处，一边ON在射线OA上，另一边OM在直线AB的下方．

（1）将图1中的三角板绕点O按顺时针方向旋转至图2的位置，使得OM落在射线OA上，此时ON旋转的角度为

90

°；
（2）继续将图2中的三角板绕点O按顺时针方向旋转至图3的位置，使得OM在∠BOC的内部，则∠BON-∠COM=

30

°；
（3）在上述直角三角板从图1旋转到图3的位置的过程中，若三角板绕点O按每秒钟15°的速度旋转，当OM恰为∠BOC的平分线时，此时，三角板绕点O的运动时间为

16

秒，简要说明理由．

Answer 1

分析：（1）根据旋转的性质知，旋转角∠MON=90°；
（2）分别求出∠BON=90°-∠BOM，∠COM=60°-∠BOM，则∠BON-∠COM=90°-∠BOM-60°+∠BOM=30°；
（3）易求∠AOM+∠AOC+∠COM′=240°，则三角板绕点O的运动时间为

240

15

=16（秒）．

解答：解：（1）如图2，依题意知，旋转角是∠MON，且∠MON=90°．
故填：90；                            

（2）如图3，∠AOC：∠BOC=2：1，
∴∠AOC=120°，∠BOC=60°，
∵∠BON=90°-∠BOM，∠COM=60°-∠BOM，
∴∠BON-∠COM=90°-∠BOM-60°+∠BOM=30°，
故填：30；      
                        
（3）16秒．理由如下：
如图4．∵点O为直线AB上一点，∠AOC：∠BOC=2：1，
∴∠AOC=120°，∠BOC=60°．
∵OM恰为∠BOC的平分线，
∴∠COM′=30°．
∴∠AOM+∠AOC+∠COM′=240°．   
∵三角板绕点O按每秒钟15°的速度旋转，
∴三角板绕点O的运动时间为

240

15

=16（秒）． 
故填：16．

点评：本题考查了旋转的性质，关键是应该认真审题并仔细观察图形，找到各个量之间的关系，并求出角的度数是解题的关键．