题目内容
若1＜x＜2，则|x-3|+
的值为
- A.2
- B.-2
- C.2x-4
- D.4-2x
A
分析：先判断出x-3与x-1的正负情况，再根据绝对值的性质与二次根式的性质化简即可．
解答：∵1＜x＜2，
∴x-3＜0，x-1＞0，
∴|x-3|+=-（x-3）+x-1=-x+3+x-1=2．
故选A．
点评：本题考查了二次根式的性质与化简，绝对值的性质，根据x的取值范围判断出x-3与x-1的正负情况是解题的关键．
分析：先判断出x-3与x-1的正负情况，再根据绝对值的性质与二次根式的性质化简即可．
解答：∵1＜x＜2，
∴x-3＜0，x-1＞0，
∴|x-3|+
=-（x-3）+x-1=-x+3+x-1=2．故选A．
点评：本题考查了二次根式的性质与化简，绝对值的性质，根据x的取值范围判断出x-3与x-1的正负情况是解题的关键．
练习册系列答案
相关题目
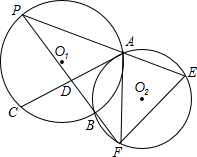、PB的延长线分别交⊙O2于点E、F，PB交AC于D．
已知△ABC中，D是AB上一点，∠BCD=∠A，若BD=1，AD=2，则BC=