Question

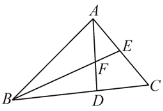
【题目】已知：如图，△ABC中，AD⊥BC于D，BE是三角形的角平分线，交AD于F．

（1）若∠ABC=40°， 求∠AFE的度数．

（2）若∠BAC是直角，请猜想：△AFE的形状，并写出证明．

Answer 1

【答案】（1）∠AFE=70°；（2）等腰三角形，证明见解析．

【解析】

（1）根据角平分线的定义求出∠DBF，再根据三角形内角和定理求出∠BFD即可解决问题．

（2）结论：△AEF是等腰三角形．想办法证明∠AEF=∠AFE即可．

（1）∵AD⊥BC，

∴∠ADB=90°，

∵∠ABC=40°，BE平分∠ABC，

∴∠DBF=∠ABC=20°，

∴∠BFD=90°-20°=70°

∴∠AFE=∠BFD=70°

（2）结论：△AEF是等腰三角形．

理由：∵∠BAE=∠ADB=90°，

∴∠AEF+∠ABE=90°，∠BFD+∠FBD=90°，

∵∠ABE=∠DBF，

∴∠AEF=∠BFD，

∵∠BFD=∠AFE，

∴∠AFE=∠AEF，

∴AE=AF，

∴△AEF是等腰三角形．