题目内容
如图：点D在AC上，∠DBC=∠A，CB=
，AC=3，求CD的长．
【答案】分析：由题中条件不难得△CBD∽△CAB，进而利用相似三角形对应边成比例，可求解线段的长．
解答：解：∵∠DBC=∠A，∠C为公共角，
∴△CBD∽△CAB，
∴
，即CB2=AC•CD
解得CD=2．
点评：熟练掌握相似三角形的判定及性质．
解答：解：∵∠DBC=∠A，∠C为公共角，
∴△CBD∽△CAB，
∴
，即CB2=AC•CD解得CD=2．
点评：熟练掌握相似三角形的判定及性质．
练习册系列答案
阅读快车系列答案
相关题目
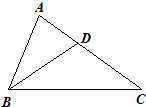21、如图，点D在AC上，且∠ABD=∠C，AB=4，CD=6，求AD的长．
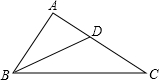如图，点D在AC上，且∠ABD=∠C，AB=CD=2，则AD=
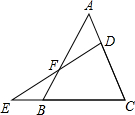如图，点D在AC上，点E在CB的延长线上，且BE=AD，ED交AB于点F，求证：EF•BC=AC•FD．
已知：如图，点O在AC上，⊙O过B，C两点，交AC于点D，AB与⊙O相切．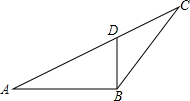
如图，点D在AC上，∠BAD=∠DBC．