Question

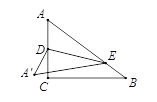
【题目】如图，在△ABC中，∠C=90°，AB=5，BC=4． 点D是边AC的中点，点E在边AB上，将△ADE沿DE翻折，使点A落在点A′处，当线段AE的长为_______时，A′E∥BC．

Answer 1

【答案】或

【解析】

根据∠C=90°，AB=5，BC=4，可得AC=3，由翻折的性质可得△ADE≌△A′DE，由平行线的性质可得，A′E⊥AC,通过图形进行计算即可解答.

解：∵C=90°，AB=5，BC=4，∴AC=3，

①当A′点在直线AB的上方时，如图所示，

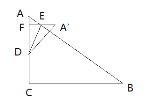
∵△ADE沿DE翻折后，A′E∥BC，

∴△ADE≌△A′DE，∴AD= A′D= ,cos∠A= cos∠A′，

则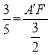 ,可得，A′F= , sin∠A= sin∠A′，可得DF= ,

∴AF=AD-DF=，

cos∠A== ,解得AE=;

②当A′点在直线AB的下方时，如图所示，

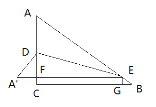
同理可得，AD= A′D=，A′F=， DF=，

∴CF=AC-AD-DF=，

∵四边形EFCG是矩形，∴EG=CF=,

sin∠B= ,解得EB=,

∴AE=AB-EB=,

故答案为：