Question

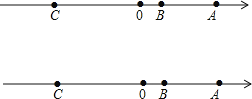
【题目】如图，已知数轴上点表示的数为，点表示的数为，是数轴上一点，且，动点从出发，以每秒个单位长度的速度沿数轴向左匀速运动，设运动时间为秒．

（1）直接写出数轴上点表示的数，并用含的代数式表示线段的长度；

（2）设是的中点，是的中点．点在运动过程中，线段的长度是否发生变化？若变化，请说出理由；若不变，求线段的长度．

（3）动点从点出发，以每秒个单位长度的速度沿数轴向左匀速运动，动点从点出发，以每秒个单位长度沿数轴向左匀速运动，若三点同时出发，当点追上点后立即返回向点运动，遇到点后则停止运动．求点从开始运动到停止运动，行驶的路程是多少个单位长度？

Answer 1

【答案】（1）点表示的数为，线段的长度为；（2）线段的长度不发生变化，其值为；（3）从开始运动到停止运动，行驶的路程是个单位长度．

【解析】

（1）点表示的数为，线段的长度为；

（2）分类讨论：①当点在点两点之间运动时；②当点运动到点的左侧时；利用中点的定义和线段的和差易求出；

（3）先求出从出发相遇时的时间，再求出相遇时之间剩余的路程的相遇时间，就可以求出一共走的时间，由的速度就可以求出点行驶的路程．

解：（1）设点表示的数为，由题意，得

，

解得．

故点表示的数为，线段的长度为；

（2）线段的长度不发生变化．

理由：分两种情况：

①当点在两点之间运动时，如图：

②当点运动到点的左边时，如图：

综上所述，线段的长度不发生变化，其值为．

（3）由题意得：

的相遇时间为：，

剩余的路程为：个单位长度，

相遇的时间为：

点走的路程为：个单位长度．

故点从开始运动到停止运动，行驶的路程是个单位长度．