题目内容

21、如图，EF∥AD，∠1=∠2，将求证AB∥DG的过程填空完整．
证明：∵EF∥AD（
已知
）
∴∠2=
∠3
（
两直线平行，同位角相等
）
又∵∠1=∠2（
已知
）
∴∠1=∠3（
等量代换
）
∴AB∥
DG
（
内错角相等，两直线平行
）
分析：此题根据平行线的性质、判定直接完成填空．两条直线平行，则同位角相等，内错角相等，同旁内角互补；反之，同位角相等，内错角相等，同旁内角互补，则两直线平行．
解答：证明：∵EF∥AD（已知）
∴∠2=∠3（两直线平行，同位角相等）
又∵∠1=∠2（已知）
∴∠1=∠3（等量代换）
∴AB∥DG（内错角相等，两直线平行）
点评：此题综合运用了平行线的性质和判定，注意等量代换的应用．
练习册系列答案
相关题目
22、如图：EF∥AD，∠1=∠2，∠BAC=70°，将求∠AGD的过程填写完整．
因为EF∥AD，
所以∠2=
∠3
．
又因为∠1=∠2，所以∠1=∠3．
所以AB∥
DG
．
所以∠BAC+
∠DGA
=180°．
又因为∠BAC=70°，
所以∠AGD=
110°
．
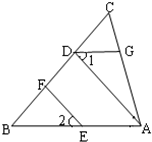8、如图，EF∥AD，∠1=∠2，∠BAC=70°．则∠AGD=
110°
．
21、请把下列解题过程补充完整并在括号中注明理由：
如图，EF∥AD，∠1=∠2，∠BAC=70°，求∠AGD．
解：∵EF∥AD，
∴∠2=
∠3
，（
两直线平行，同位角相等
）
又∵∠1=∠2，
∴∠1=∠3，
∴AB∥
DG
，（
内错角相等，两直线平行
）
∴∠BAC+
∠AGD
=180°，（
两直线平行，同旁内角互补
）
∵∠BAC=70°，
∴∠AGD=
110°
．
22、补全下面推理过程：
（1）如图，已知∠B=∠CDF，∠E+∠ECD=180°，证明：AB∥EF．
证明：∵∠B=∠CDF
∴
AB
∥
CD
（同位角相等，两直线平行）
∵∠E+∠ECD=180°
∴
CD
∥
EF
（同旁内角互补，两直线平行）
∴AB∥EF（平行于同一条直线的两直线互相平行）
（2）如图，EF∥AD，∠ADG=∠BEF，∠BAC=70°，求∠AGD的度数．
解：∵EF∥AD
∴∠BEF=
∠BAD
（
两直线平行，同位角相等
）
又∵∠ADG=∠BEF
∴∠ADG=∠DAB
∴AB∥
DG
（
内错角相等，两直线平行
）
∴∠BAC+
∠AGD
=180°（
两直线平行，同旁内角互补
）
又∵∠BAC=70°，
∴∠AGD=
110°
．
如图，EF∥AD，∠1=∠2，将求证AB∥DG的过程填空完整．
证明：∵EF∥AD（
已知
已知
）∴∠2=
∠3
∠3
（
两直线平行，同位角相等
两直线平行，同位角相等
）又∵∠1=∠2（
已知
已知
）∴∠1=∠3（
等量代换
等量代换
）∴AB∥
DG
DG
（
内错角相等，两直线平行
内错角相等，两直线平行
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网