Question

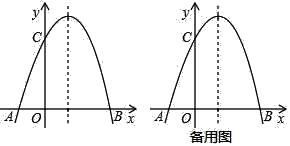
【题目】已知，抛物线y=﹣x2+bx+c经过点A（﹣1，0）和C（0，3）．

（1）求抛物线的解析式；

（2）设点M在抛物线的对称轴上，当△MAC是以AC为直角边的直角三角形时，求点M的坐标．

Answer 1

【答案】（1）y=﹣x2+2x+3；（2）当△MAC是直角三角形时，点M的坐标为（1，）或（1，﹣）．

【解析】

（1）由点A、C的坐标，利用待定系数法即可求出抛物线的解析式；

（2）设点M的坐标为（1，m），则CM=，AC=，AM=，分∠ACM=90°和∠CAM=90°两种情况，利用勾股定理可得出关于m的方程，解之可得出m的值，进而即可得出点M的坐标．

（1）将A（﹣1，0）、C（0，3）代入y=﹣x2+bx+c中，

得：，

解得：，

∴抛物线的解析式为y=﹣x2+2x+3．

（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，

设点M的坐标为（1，m），

则CM=，AC==，AM=．

分两种情况考虑：

①当∠ACM=90°时，有AM2=AC2+CM2，即4+m2=10+1+（m﹣3）2，

解得：m=，

∴点M的坐标为（1，）；

②当∠CAM=90°时，有CM2=AM2+AC2，即1+（m﹣3）2=4+m2+10，

解得：m=﹣，

∴点M的坐标为（1，﹣）．

综上所述：当△MAC是直角三角形时，点M的坐标为（1，）或（1，﹣）．