题目内容
 如图,直线l过边长为13的正方形ABCD的顶点B,点A、C到直线l的距离分别是5和12,则五边形AEFCD的面积是
如图,直线l过边长为13的正方形ABCD的顶点B,点A、C到直线l的距离分别是5和12,则五边形AEFCD的面积是229
229
.分析:先由条件可以得出△ABE≌△BCF,由勾股定理就可以得出AB的值,分别求出正方形的面积和两个三角形的面积就可以得出结论.
解答:解:∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°.
∴∠EAB+∠ABE=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°
∴∠ABE+∠CBF=90°.
∴∠EAB=∠FBC.
在△ABE和△BCF中,
,
∴△ABE≌△BCF,
∴BE=CF=12.
∵AE=5,在Rt△ABE中,由勾股定理,得
AB=13,
∴S正方形ABCD=13×13=169,
∴S五边形AEFCD=169+12×5×
×2=229.
故答案为:229.
∴∠AEB=∠BFC=90°.
∴∠EAB+∠ABE=90°.
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°
∴∠ABE+∠CBF=90°.
∴∠EAB=∠FBC.
在△ABE和△BCF中,
|
∴△ABE≌△BCF,
∴BE=CF=12.
∵AE=5,在Rt△ABE中,由勾股定理,得
AB=13,
∴S正方形ABCD=13×13=169,
∴S五边形AEFCD=169+12×5×
| 1 |
| 2 |
故答案为:229.
点评:本题考查了正方形的性质的运用,直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用.解答时得出三角形全等是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
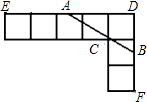 如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.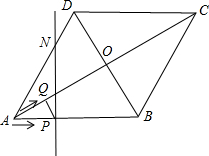 如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2
如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2 如图,直线l过边长为13的正方形ABCD的顶点B,点A、C到直线l的距离分别是5和12,则五边形AEFCD的面积是________.
如图,直线l过边长为13的正方形ABCD的顶点B,点A、C到直线l的距离分别是5和12,则五边形AEFCD的面积是________.