题目内容
(1)计算:3-2+(-2010π)0- cos30°;
cos30°;
(2)已知a=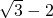 ,求代数式
,求代数式 +
+ 的值;
的值;
(3)解方程:2x2-3x=1.
解:(1)原式= +1-3
+1-3 ×
×
= +1-
+1-
=- ;
;
(2)原式= -
-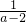
=
=
= ,
,
当a= -2时,原式=
-2时,原式= =
= ;
;
(3)2x2-3x=1,
整理得:2x2-3x-1=0,
这里a=2,b=-3,c=-1,
∵△=b2-4ac=9+8=17,
∴x= ,
,
则x1= ,x2=
,x2= .
.
分析:(1)原式第一项利用负指数公式化简,第二项利用零指数公式化简,第三项利用特殊角的三角函数值化简,计算即可得到结果;
(2)将所求式子第一项分母利用平方差公式分解因式,第二项提取-1变形,通分并利用同分母分式的加法法则计算,得到最简结果,将a的值代入即可求出值;
(3)将方程整理为一般形式,找出a,b及c的值,计算出根的判别式的值大于0,代入求根公式即可求出解.
点评:此题考查了解一元二次方程,以及实数的混合运算,涉及的知识有:零指数公式,负指数公式,分式的加减运算,以及分式的乘除运算,熟练掌握公式是解本题的关键.
 +1-3
+1-3 ×
×
=
 +1-
+1-
=-
 ;
;(2)原式=
 -
-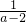
=

=

=
 ,
,当a=
 -2时,原式=
-2时,原式= =
= ;
;(3)2x2-3x=1,
整理得:2x2-3x-1=0,
这里a=2,b=-3,c=-1,
∵△=b2-4ac=9+8=17,
∴x=
 ,
,则x1=
 ,x2=
,x2= .
.分析:(1)原式第一项利用负指数公式化简,第二项利用零指数公式化简,第三项利用特殊角的三角函数值化简,计算即可得到结果;
(2)将所求式子第一项分母利用平方差公式分解因式,第二项提取-1变形,通分并利用同分母分式的加法法则计算,得到最简结果,将a的值代入即可求出值;
(3)将方程整理为一般形式,找出a,b及c的值,计算出根的判别式的值大于0,代入求根公式即可求出解.
点评:此题考查了解一元二次方程,以及实数的混合运算,涉及的知识有:零指数公式,负指数公式,分式的加减运算,以及分式的乘除运算,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
