题目内容
从如图所示的二次函数y=ax2+bx+c的图象中，孔明同学观察得出了下面四条信息：①b2﹣4ac＞0；②c＞1；（3）2a﹣b＜0；（4）a+b+c＜0．你认为其中错误的有（ ）
A．1个 B．2个 C．3个 D．4个
A【考点】二次函数图象与系数的关系．
【分析】根据抛物线与x轴的交点情况判断b2﹣4ac的符号；根据抛物线与y轴的交点判断c的大小；根据开口方向和对称轴，判断2a﹣b的符号；根据x=1时，y＜0，判断a+b+c的符号．
【解答】解：（1）根据图象，该函数图象与x轴有两个交点，
∴△=b2﹣4ac＞0；
故（1）正确；
（2）由图象知，该函数图象与y轴的交点在点（0，1）的下方，
∴c＜1；
故（2）错误；
（3）对称轴x=﹣
＞﹣1；
又∵函数图象的开口方向向下，
∴a＜0，
∴﹣b＜﹣2a，即2a﹣b＜0，
故（3）正确；
（4）根据图示可知，当x=1时，即y=a+b+c＜0，
故（4）正确．
故选：A．
【点评】本题考查的是二次函数图象与系数的关系，掌握二次函数的性质、灵活运用数形结合思想是解题的关键，解答时，要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式．
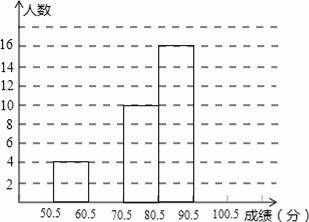
为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有850名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）进行统计．请你根据尚未完成并有局部污染的频率分布表和频率分布直方图，解答下列问题：
| 分 组 | 频数 | 频率 |
| 50.5～60.5 | 4 | 0.08 |
| 60.5～70.5 |
| 0.16 |
| 70.5～80.5 | 10 |
|
| 80.5～90.5 | 16 | 0.32 |
| 90.5～100.5 |
|
|
| 合 计 | 50 | 1.00 |
（1）填充频率分布表的空格；
（2）补全频数直方图，并在此图上直接绘制频数分布折线图；
（3）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？
（4）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？
B．
C．
D．
的图象经过点P（a+1，4），则a= ．
）•ω=1，则ω=__________．