题目内容
 如图是由四个大小不等的、顶角为120°的等腰三角形拼接而成.已知三角形ABC面积为100,三角形ACD面积为32,三角形ABF的面积为37.组成图形的四个等腰三角形中,最小的一个面积为
如图是由四个大小不等的、顶角为120°的等腰三角形拼接而成.已知三角形ABC面积为100,三角形ACD面积为32,三角形ABF的面积为37.组成图形的四个等腰三角形中,最小的一个面积为分析:设△ABC的高为h,由已知三角形ABC面积为100,求得h2=
①,再分别求出BF,CM的长,然后可得MN的长,再根据勾股定理求出△NME的高,然后求得三角形MNE的关系式②,将①代入②即可.
100
| ||
| 3 |
解答:解:设△ABC的高为h,由已知三角形ABC面积为100,
可得h2=
①,
设S△ABF的高为x,则x=
,
由sin60°=
,得BF=
∴BN=
,同理可得CM=
,
MN=2
h-
,
△NME的高为(2
h-
)×
,
S△MNE=
×(2
h-
)×(2
h-
)×
②,
将①代入②得S△MNE=9.61.
故答案为:9.61.
可得h2=
100
| ||
| 3 |
设S△ABF的高为x,则x=
| 37 |
| h |
由sin60°=
| x |
| BF |
| 74 | ||
|
∴BN=
| 74 |
| h |
| 64 |
| h |
MN=2
| 3 |
| 138 |
| h |
△NME的高为(2
| 3 |
| 138 |
| h |
| 1 | ||
2
|
S△MNE=
| 1 |
| 2 |
| 3 |
| 138 |
| h |
| 3 |
| 138 |
| h |
| 1 | ||
2
|
将①代入②得S△MNE=9.61.
故答案为:9.61.
点评:此题主要考查学生对等腰三角形的性质,三角形面积,勾股定理的理解和掌握,此题步骤繁琐,计算时数值精确,没有一处保留,此题难度较大,稍有疏忽,就可能导致错误,属于难题.

练习册系列答案
相关题目
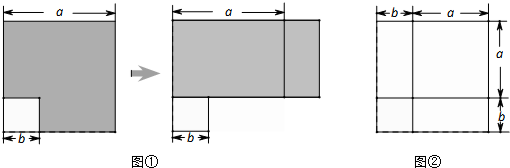
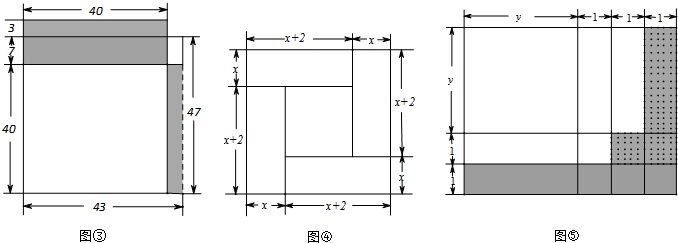




 ,宽为
,宽为 的矩形,构造图④
的矩形,构造图④
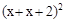 或四个长
或四个长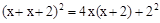




 的解
的解 与
与 的大小关系(其中
的大小关系(其中 )?
)? ,宽
,宽 的矩形,按图⑤方式分割
的矩形,按图⑤方式分割

 ,
, ,即
,即 ,
,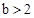 时,表示
时,表示 与
与 的大小关系
的大小关系 ,
,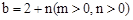 ,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长)
,要求参照上述研究方法,画出示意图,并写出几何建模步骤(用钢笔或圆珠笔画图,并标注相关线段的长) 如图是由四个大小不等的、顶角为120°的等腰三角形拼接而成.已知三角形ABC面积为100,三角形ACD面积为32,三角形ABF的面积为37.组成图形的四个等腰三角形中,最小的一个面积为________.
如图是由四个大小不等的、顶角为120°的等腰三角形拼接而成.已知三角形ABC面积为100,三角形ACD面积为32,三角形ABF的面积为37.组成图形的四个等腰三角形中,最小的一个面积为________.