题目内容
一枚质地均匀的正方体骰子,其六个面上分别刻有1、2、3、4、5、6六个数字,投掷这个骰子一次,则向上一面的数字小于3的概率是( )
A. 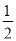 B.
B. 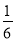 C.
C. 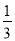 D.
D. 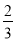
练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
题目内容
一枚质地均匀的正方体骰子,其六个面上分别刻有1、2、3、4、5、6六个数字,投掷这个骰子一次,则向上一面的数字小于3的概率是( )
A. 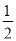 B.
B. 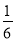 C.
C. 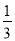 D.
D. 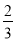
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案