题目内容
 (2012•张家口一模)如图,已知△ABC中,∠ABC=45°,AD是BC边上的高,
(2012•张家口一模)如图,已知△ABC中,∠ABC=45°,AD是BC边上的高,(1)尺规作图:在∠ABC的内部作∠CBM,使得∠CBM=∠DAC(要求:只保留作图痕迹,不写作法和证明);
(2)若射线BM与AC交于点E,与AD交于点F,且CD=3,试求线段DF的长.
分析:(1)作∠CBM=∠ADE,其中BM交AC于E、AD于F;
(2)根据等腰直角三角形的性质可得AD=BD,由ASA可证△BDF≌△ADC,再根据全等三角形的性质求解.
(2)根据等腰直角三角形的性质可得AD=BD,由ASA可证△BDF≌△ADC,再根据全等三角形的性质求解.
解答: 解:(1)作图如图1:
解:(1)作图如图1:
(2)如图2:
∵AD⊥BC,∠ABC=45°
∴∠1=∠ABC=45°
∴AD=BD
在△BDF和△ADC中
∵
,
∴△BDF≌△ADC(ASA)
∴DF=DC=3
 解:(1)作图如图1:
解:(1)作图如图1:(2)如图2:
∵AD⊥BC,∠ABC=45°
∴∠1=∠ABC=45°
∴AD=BD
在△BDF和△ADC中
∵
|
∴△BDF≌△ADC(ASA)
∴DF=DC=3
点评:综合考查了角的作图,全等三角形的判定和性质的知识,三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
相关题目
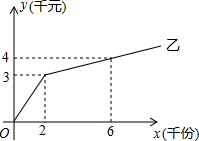 (2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表:
(2012•张家口一模)某单位准备印制一批书面材料,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的印刷费用y(千元)与书面材料数量x(千份)的关系见下表: (1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;
(1)求抽取的学生人数,并根据抽查到的学生五个等级人数的分布情况,补全扇形统计图和频数分布直方图;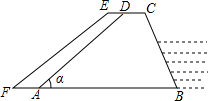 (2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.
(2012•张家口一模)如图,梯形ABCD是一个拦河坝的截面图,坝高为6米.背水坡AD的坡度i为1:1.2,为了提高河坝的抗洪能力,防汛指挥部决定加固河坝,若坝顶CD加宽0.8米,新的背水坡EF的坡度为1:1.4.河坝总长度为4800米.