题目内容
当（x-3）2+|y+4|=0时，xy-y2的值是
- A.28
- B.4
- C.-28
- D.-4
C
分析：根据非负数的性质，可求出x、y的值，然后将其代入代数式计算即可．
解答：∵（x-3）2+|y+4|=0，
∴（x-3）2=0，|y+4|=0，
∴x=3，y=-4，
∴xy-y2=-12-16=-28，
故选C．
点评：本题考查了非负数的性质：偶次方具有非负性．任意一个数的偶次方都是非负数，当几个数或式的偶次方相加和为0时，则其中的每一项都必须等于0．任意一个数的绝对值都是非负数，当几个数或式的绝对值相加和为0时，则其中的每一项都必须等于0．
分析：根据非负数的性质，可求出x、y的值，然后将其代入代数式计算即可．
解答：∵（x-3）2+|y+4|=0，
∴（x-3）2=0，|y+4|=0，
∴x=3，y=-4，
∴xy-y2=-12-16=-28，
故选C．
点评：本题考查了非负数的性质：偶次方具有非负性．任意一个数的偶次方都是非负数，当几个数或式的偶次方相加和为0时，则其中的每一项都必须等于0．任意一个数的绝对值都是非负数，当几个数或式的绝对值相加和为0时，则其中的每一项都必须等于0．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目
如图，在△ABC中，已知AB=BC=CA=4cm，AD⊥BC于D．点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点Q沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x（s）．
水管．如图表示水塔中的储水量Q（米3）与时间t（小时）之间的函数图象．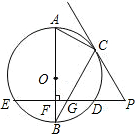
？试写出你的猜想，并说明理由．
