题目内容
【题目】在平面直角坐标系中,点![]() 的坐标分别是点
的坐标分别是点![]() ,
,![]() ,且
,且![]() 满足:
满足:![]() .
.
(1)则![]() _________,
_________,![]() _________;
_________;
(2)![]() 为
为![]() 轴负半轴上一点,过点
轴负半轴上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
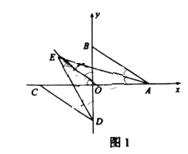
①如图1,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 的度数;
的度数;
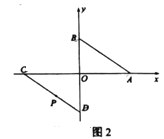
②如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,求
上一点,求![]() 之间满足的关系式.
之间满足的关系式.
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)利用绝对值和二次根式的非负性可得a、b的值;
(2)①如下图,根据![]() 和
和![]() ,可得∠CDO+∠BAO=90°,从而推导得出∠AED;
,可得∠CDO+∠BAO=90°,从而推导得出∠AED;
②如下图,将直线![]() 平移到
平移到![]() 处,
处,![]() 对应
对应![]() ,
,![]() 对应
对应![]() ,根据△COD的面积关系,可得出点D的坐标;然后在△COD的面积还等于③+④可得到m、n的关系.
,根据△COD的面积关系,可得出点D的坐标;然后在△COD的面积还等于③+④可得到m、n的关系.
(1)∵![]()
∴![]()
∴![]() ,
,![]()
(2)①分别作![]() ,
,![]() .
.
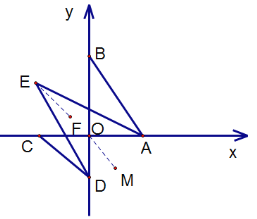
则![]() ,
,![]() .
.
设∠CDE=x,∠BAE=y
∴![]()
∴![]()
则![]() .
.
②设![]() .
.
将直线![]() 平移到
平移到![]() 处,
处,![]() 对应
对应![]() ,
,![]() 对应
对应![]()
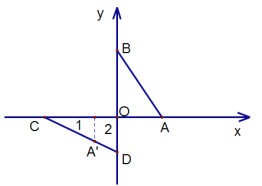
则![]()
已知![]() 、
、![]() 坐标,则直线
坐标,则直线![]() 与
与![]() 轴交点为
轴交点为![]() .
.
由![]() 可得:
可得:![]() .
.
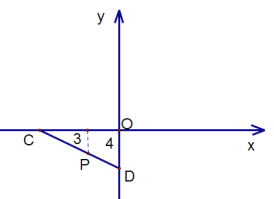
根据![]() ,即:
,即:![]()
解得![]() .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目