题目内容
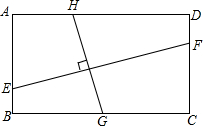如图，E、F、G、H分别在矩形ABCD上，EF⊥GH，若AB=2，BC=3，则EF与GH的比值是多少？
分析：若要求EF与GH的比值，可把EF和GH放置在不同的三角形中，过E作EK⊥CD交CD于K，过H作HI⊥BC交BC于I，得Rt△EFK和Rt△HGI再证明两三角形相似，可求的EF与GH的比值．
解答：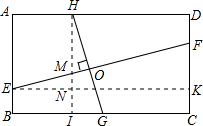
解：过E作EK⊥CD交CD于K，过H作HI⊥BC交BC于I，
∴∠EKF=∠HIG=90°，HI∥AB，EK∥BC，
∵EF⊥GH，HI⊥EK，
∴∠HOM=∠MNE=90°．
又∵∠EMN=∠HMO，
∴∠MEN=∠MHO．
∴△EFK∽△HGI（AAS）．
∴
=
．
由题意知：EK=BC=3，HI=AB=2，
∴
=
．
解：过E作EK⊥CD交CD于K，过H作HI⊥BC交BC于I，∴∠EKF=∠HIG=90°，HI∥AB，EK∥BC，
∵EF⊥GH，HI⊥EK，
∴∠HOM=∠MNE=90°．
又∵∠EMN=∠HMO，
∴∠MEN=∠MHO．
∴△EFK∽△HGI（AAS）．
∴
| EF |
| HG |
| EK |
| HI |
由题意知：EK=BC=3，HI=AB=2，
∴
| EF |
| HG |
| 3 |
| 2 |
点评：本题考查相似三角形的判断和性质，三角形相似的判定一直是中考考查的热点之一，在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用．有时还要通过作辅助线构造相似三角形．
练习册系列答案
相关题目
14、如图，已知⊙P的半径OD=5，OD⊥AB，垂足是G，OG=3，则弦AB=
如图，已知A，B两点是反比例函数y=
如图AB是⊙O的直径，⊙O过BC的中点D，且DE⊥AC于点E．