Question

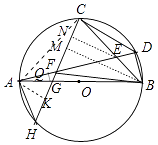
【题目】如图1，已知AB为⊙O的直径，点C为 的中点，点D在 上，连接BD、CD、BC、AD、BC与AD相交于点E．
（1）求证：∠C+∠CBD=∠CBA；
（2）如图2，过点C作CD的垂线，分别与AD，AB，⊙O相交于点F、G、H，求证：AF=BD；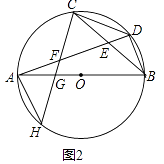
（3）如图3，在（2）的条件下，连接BF，若BF=BC，△CEF的面积等于3，求FG的长．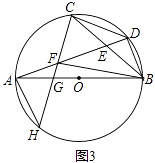

Answer 1

【答案】
（1）证明：连接AC，

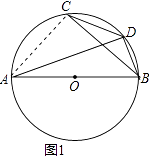
在⊙O中，∵C为 的中点，

∴ = ，

∴∠CBA=∠CAB=∠CAD+∠DAB，

∵ = ， = ，

∴∠DCB=∠DAB，∠CBD=∠CAD，

∴∠DCB+∠CBD=∠CAD+∠DAB=∠CAB=∠CBA

（2）证明：连接AC．

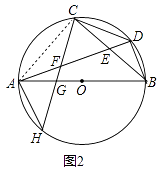
∵AB是直径，

∴∠ACB=90°=∠ACF+∠FCB，

∵CD⊥CH，

∴∠DCH=90°=∠FCB+∠DCB，

∴∠ACF=∠DCB，

∵ = ，

∴AC=BC，

在△ACF和△BCD中，

，

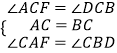∴△ACF≌△BCD，

∴AF=BD

（3）解：作BM⊥CH于M，AK⊥CH于K．

∴∠ACK+∠CAK=90°，∠AKC=∠BMC=90°，

∵∠ACB=90°，

∴∠ACK+∠KCB=90°，

∴∠CAK=∠KCB，∵AC=BC，

∴△ACK≌△CNM，

∴AK=CM，

∵CB=BF，BM⊥CF，

∴CM=FM=AK，

∵△ACF≌△BCD，

∴CF=CD，

∵∠FCD=90°，

∴∠CFD=∠CDF=45°=∠AFK，

∴△AFK是等腰直角三角形，

∴AK=FK=FM=CM，

在Rt△AKC中，tan∠CAK= =3，作EN⊥CH于N，

在Rt△NCE中，∵∠HCB=∠CAK，

∴tan∠NCE= =3，设CN=m，EN=3m=NF，

∴S△CEF= CFEN= ×（m+3m）×3m=3，

∴m= ，

∴CF=4m=2 ，

∴CM=FM=FK=AK= ，

∴AF=2，

∵ = ，

∴∠DCB=∠DAB=∠ACK，

过G作GQ⊥AF于Q，

在Rt△AQG中，tan∠FAB= = ，设QG=x，AQ=3x，FQ=x，

∴4x=2，

∴x= ，

∴FG= x=

【解析】（1）连接AC．由 = ，推出∠CBA=∠CAB=∠CAD+∠DAB，由 = ， = ，推出∠DCB=∠DAB，∠CBD=∠CAD，推出∠DCB+∠CBD=∠CAD+∠DAB=∠CAB=∠CBA．（2）只要证明△ACF△BCD，即可推出AF=BD．（3）由△ACK≌△CNM，推出AK=CM，由△ACF≌△BCD，推出CF=CD，△AFK是等腰直角三角形，推出AK=FK=FM=CM，在Rt△AKC中，tan∠CAK= =3，作EN⊥CH于N，在Rt△NCE中，由∠HCB=∠CAK，推出tan∠NCE= =3，设CN=m，EN=3m=NF，由S△CEF= CFEN= ×（m+3m）×3m，推出m= ，推出CF=4m=2 ，推出CM=FM=FK=AK= ，AF=2，由 = ，推出∠DCB=∠DAB=∠ACK，过G作GQ⊥AF于Q，在Rt△AQG中，tan∠FAB= = ，设QG=x，AQ=3x，FQ=x，可得4x=2，得x= ，再根据FG= QG即可解决问题．