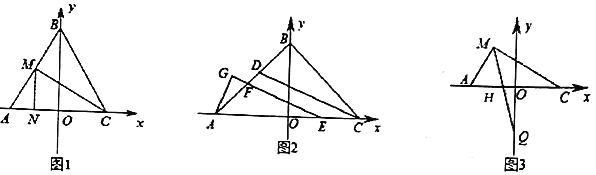
题目内容
【题目】在平面直角坐标系中,已知![]() ,
,![]() ,
,![]() .
.
(1)如图1,若![]() ,
,![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,则
,则![]() _____.
_____.
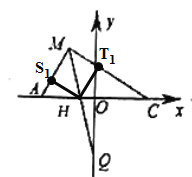
(2)如图2,若![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点
于点![]() ,过
,过![]() 上一点作
上一点作![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的高,探究
的高,探究![]() 与
与![]() 的数量关系;
的数量关系;
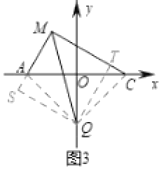
(3)如图3,在(1)的条件下,![]() 上点
上点![]() 满足
满足![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先证明△ABC是等边三角形,然后得到点M是AB的中点,则点N为AO的中点,即可得到A点坐标,求出m的值;
(2)先求出m=n,得到△AOB是等腰直角三角形,然后得到△ABC也是等腰直角三角,则∠ACB=45°,从而得到∠AEG=22.5°,延长![]() 到
到![]() ,使
,使![]() ,连
,连![]() 交
交![]() 于
于![]() ,证明△AEH和△AER是等腰三角形,则得到AR=ER,AH=2AG,然后根据全等得到AH=EF,即可得到
,证明△AEH和△AER是等腰三角形,则得到AR=ER,AH=2AG,然后根据全等得到AH=EF,即可得到![]() ;
;
(3)先证明MQ是∠AMC的角平分线,作![]() 于
于![]() ,
,![]() 于
于![]() ,证明
,证明![]() ≌
≌![]() ,则得到
,则得到![]() ,则
,则![]() ,然后得到OQ=OA,由(1)的结论,即可求出Q点坐标.
,然后得到OQ=OA,由(1)的结论,即可求出Q点坐标.
解:(1)∵![]() ,
,![]() ,
,
∴AO=CO=m,
∴AB=BC=AC,
∴△ABC是等边三角形,
∵![]() ,
,
∴点M是AB的中点,
∵![]() 轴,
轴,
∴点N是AO的中点,
∵点N为![]() ,
,
∴点A为:![]() ,
,
∴![]() ;
;
故答案为:4.
(2)![]()
证明:∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∵点![]() 与点
与点![]() 关于
关于![]() 轴对称
轴对称
∴![]()
∴![]()
∴![]()
∴![]()
∵![]() 平分
平分![]()
∴![]()
∵![]()
∴![]()
延长![]() 到
到![]() ,使
,使![]() ,连
,连![]() 交
交![]() 于
于![]()
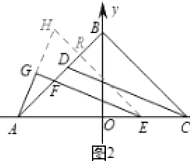
∵![]() 是
是![]() 的高.
的高.
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() ,
,![]()
∴![]()
在![]() 和
和![]() 中,
中,
∵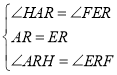
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
∵![]()
∴![]()
(3)作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
由面积法及![]() ,
,
可得![]()
∴![]() 平分
平分![]()
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∴![]()
连接![]() ,则
,则![]()
在![]() 和
和![]() 中,
中,
∵![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
由(1)知![]()
∴![]()
∴![]()
∴![]()

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目