题目内容
如图，弦AB和CD相交于点P，∠B=30°，∠APD=80°，则∠A等于
- A.30°
- B.50°
- C.70°
- D.100°
C
分析：根据对顶角相等可得∠BPC=∠APD=80°，而∠B=30，再结合三角形内角和定理可求∠C，根据同弧所对的圆周角相等易求∠C．
解答：
解：如右图，
∵∠BPC=∠APD=80°，∠B=30，
∴∠C=180°-80°-30°=70°，
∴∠A=∠C=70°．
故选C．
点评：本题考查了圆周角定理、对顶角相等、三角形内角和定理，解题的关键是求出∠C．
分析：根据对顶角相等可得∠BPC=∠APD=80°，而∠B=30，再结合三角形内角和定理可求∠C，根据同弧所对的圆周角相等易求∠C．
解答：
解：如右图，∵∠BPC=∠APD=80°，∠B=30，
∴∠C=180°-80°-30°=70°，
∴∠A=∠C=70°．
故选C．
点评：本题考查了圆周角定理、对顶角相等、三角形内角和定理，解题的关键是求出∠C．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
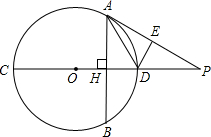如图，AB为⊙O内垂直于直径的弦，AB、CD相于点H，△AED与△AHD关于直线AD成轴对称．
