题目内容
【题目】学习新知：如图 1、图 2，
是矩形
所在平面内任意一点，则有以下重要结论： 
．该结论的证明不难，同学们通过勾股定理即可证明．
应用新知：如图 3，在
中，
，
，
是 内一点，且
,
，则
的最小值为__________．
【答案】
【解析】
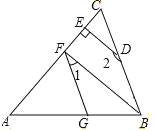
过点A作AE⊥AD，过点B作BE⊥BD，AE与BE交于点E，连接DE、CE，如图，则易得四边形ADBE为矩形，可得AB=DE，于是求
的最小值就转化为求DE的最小值，由题意中的结论知
，于是CE的长可求，然后再根据三角形的三边关系可得当C、D、E三点共线时，DE取得最小值，问题即得解决．
解：过点A作AE⊥AD，过点B作BE⊥BD，AE与BE交于点E，连接DE、CE，如图，
则四边形ADBE为矩形，∴AB=DE，
由题意中的结论知：，即
，
解得：
，
在△CDE中，由三角形的三边关系可得：
，
∴当C、D、E三点共线时，
，此时DE取最小值为，
即的最小值为．
故答案为：．
练习册系列答案
相关题目
