题目内容
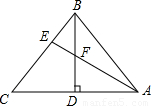
 已知:BF为∠ABC的角平分线,CF为外角∠ACG的角平分线,求:∠F与∠A的关系.
已知:BF为∠ABC的角平分线,CF为外角∠ACG的角平分线,求:∠F与∠A的关系.
分析:根据角平分线的性质可得∠1=∠2,∠3=∠4,然后利用三角形的外角的性质分别用含有∠A和∠F的式子表示出∠2,从而不难求得∠F与∠A的关系.
解答: 解:∵BF为∠ABC的角平分线,CF为外角∠ACG的角平分线.
解:∵BF为∠ABC的角平分线,CF为外角∠ACG的角平分线.
∴∠1=∠2,∠3=∠4.
∵∠ACG=∠A+∠ABC.
即2∠2=∠A+2∠3.
∴∠2=
∠A+∠3.
∵∠2=∠F+∠3.
∴∠F=
∠A.
 解:∵BF为∠ABC的角平分线,CF为外角∠ACG的角平分线.
解:∵BF为∠ABC的角平分线,CF为外角∠ACG的角平分线.∴∠1=∠2,∠3=∠4.
∵∠ACG=∠A+∠ABC.
即2∠2=∠A+2∠3.
∴∠2=
| 1 |
| 2 |
∵∠2=∠F+∠3.
∴∠F=
| 1 |
| 2 |
点评:此题主要考查:(1)三角形的外角性质:三角形的一个外角等于和它不相邻的两个内角的和.
(2)角平分线的定义.
(2)角平分线的定义.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
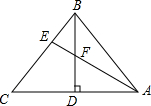 (2012•南岗区二模)已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为
(2012•南岗区二模)已知:BD为△ABC边AC上的高,E为BC上一点,CE=2BE,∠CAE=30°,若EF=3,BF=4,则AF的长为 已知:BF为∠ABC的角平分线,CF为外角∠ACG的角平分线,求:∠F与∠A的关系.
已知:BF为∠ABC的角平分线,CF为外角∠ACG的角平分线,求:∠F与∠A的关系.