Question

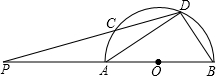
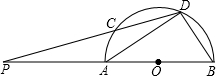已知如图，AB为半圆的直径，C、D为半圆弧上的两点，若弧CD=弧BD，DC与BA的延长线交于P，如果，AP：CP=3：4，△ADB的面积为，则AP的长为________．

Answer 1

分析：连OD、AC可以根据平行线分线段成比例定理的逆定理证明AC∥OD，则CD即可利用圆的半径表示出来，进而表示出BD，在直角△ABD中利用勾股定理即可求得AD，再根据△ADB的面积为可以得到关于半径的方程求得圆的半径，利用切割线定理即可求解．
解答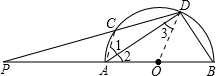：解：设AO=R，连OD、AC．
∵=
∴∠1=∠2，
又∵∠2=∠3，
∴∠1=∠3，
∴AC∥OD，
∴==，
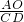∴CD=R，
∴BD=R，
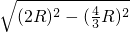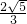∴AD===R，
由S_△AOB=16，
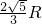
得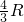：•=16，
∴R=6，
∵PA•PB=PC•PD，设PA=x，则x（x+12）=x（x+8），
∴x=．
故PA=．
点评：本题主要考查了切割线定理，勾股定理，证得AC∥OD，利用半径表示出BD的长，利用勾股定理求得圆的半径是解题的关键．