题目内容
已知抛物线y=ax2-4ax+c与y轴交于点A（0，3），点B是抛物线上的点，且
满足AB∥x轴，点C是抛物线的顶点．（1）求抛物线的对称轴及B点坐标；
（2）若抛物线经过点（-2，0），求抛物线的表达式；
（3）对（2）中的抛物线，点D在线段AB上，若以点A、C、D为顶点的三角形与△AOC相似，试求点D的坐标．
分析：（1）先根据题意得出x=-
，求出对称轴为直线x=2；知道点A的坐标，点B是抛物线上的点AB∥x轴，即可求出抛物线的对称轴及B点坐标
（2）根据抛物线经过点（0，3），（-2，0），所以有
，解出a、c的值，即可求出抛物线的表达式．
（3）先根据抛物线的对称轴为直线x=2，求出C的坐标，再过点C作CE⊥y轴，垂足为点E，设对称轴与AB交于点F．
求出EOC∽△FAC，∠AOC=∠CAF，当△AOC∽△DAC时，求出AO、CO、AC的值，最后求出AD=
，D(
，3)；当△AOC∽△CAD时，再求出AD的值，最后求出点D的坐标即可．
| -4a |
| 2a |
（2）根据抛物线经过点（0，3），（-2，0），所以有
|
（3）先根据抛物线的对称轴为直线x=2，求出C的坐标，再过点C作CE⊥y轴，垂足为点E，设对称轴与AB交于点F．
求出EOC∽△FAC，∠AOC=∠CAF，当△AOC∽△DAC时，求出AO、CO、AC的值，最后求出AD=
| 3 |
| 2 |
| 3 |
| 2 |
解答：解：（1）由题意得，x=-
，
∴对称轴为直线x=2；
∵点A（0，3），点B是抛物线上的点，AB∥x轴，
∴AB被直线x=2垂直平分，
∴B（4，3）．
（2）∵抛物线经过点（0，3），（-2，0），所以有
，
解得
，∴抛物线的表达式为y=-
x2+x+3．
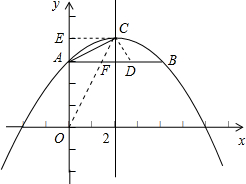
（3）∵抛物线的对称轴为直线x=2，
∴C（2，4），
过点C作CE⊥y轴，垂足为点E，设对称轴与AB交于点G，
连接OC，交AB与点F，
∵AB∥x轴，∴∠CEA=90°，∴∠CEO=∠CGA，
又∵
=
=
，
=
，∴
=
，
∴△EOC∽△GAC，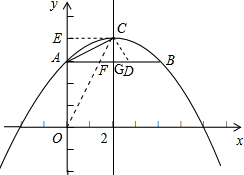
∴∠AOC=∠CAG，
当△AOC∽△DAC时，有
=
，
∵AO=3，CO=2
，AC=
，
∴AD=
，∴D(
，3)；
当△AOC∽△CAD时，有
=
，
∴AD=
，∴D(
，3)，
∴点D的坐标为(
，3)或(
，3)．
| -4a |
| 2a |
∴对称轴为直线x=2；
∵点A（0，3），点B是抛物线上的点，AB∥x轴，
∴AB被直线x=2垂直平分，
∴B（4，3）．
（2）∵抛物线经过点（0，3），（-2，0），所以有
|
解得
|
| 1 |
| 4 |
（3）∵抛物线的对称轴为直线x=2，
∴C（2，4），
过点C作CE⊥y轴，垂足为点E，设对称轴与AB交于点G，
连接OC，交AB与点F，
∵AB∥x轴，∴∠CEA=90°，∴∠CEO=∠CGA，
又∵
| CE |
| OE |
| 2 |
| 4 |
| 1 |
| 2 |
| CG |
| AG |
| 1 |
| 2 |
| CE |
| OE |
| CG |
| AG |
∴△EOC∽△GAC，
∴∠AOC=∠CAG，
当△AOC∽△DAC时，有
| AO |
| AD |
| CO |
| AC |
∵AO=3，CO=2
| 5 |
| 5 |
∴AD=
| 3 |
| 2 |
| 3 |
| 2 |
当△AOC∽△CAD时，有
| AO |
| AC |
| CO |
| AD |
∴AD=
| 10 |
| 3 |
| 10 |
| 3 |
∴点D的坐标为(
| 3 |
| 2 |
| 10 |
| 3 |
点评：本题主要考查了函数和相似三角形的综合应用问题，解题时要注意分类讨论和数形结合的思想方法．
练习册系列答案
相关题目
与x轴的另一个交点为E．
如图，已知抛物线y=ax2+bx+c（其中b＞0，c＜0）的顶点P在x轴上，与y轴交于点Q，过坐标原点O，作OA⊥PQ，垂足为A，且OA=