题目内容
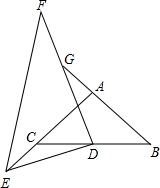 如图,△ABC是等腰直角三角形,△DEF是一个含30°角的直角三角形,将D放在BC的中点上,转动△DEF,设DE,DF分别交AC,BA的延长线于E,G,则下列结论:
如图,△ABC是等腰直角三角形,△DEF是一个含30°角的直角三角形,将D放在BC的中点上,转动△DEF,设DE,DF分别交AC,BA的延长线于E,G,则下列结论:
①AG=CE
②DG=DE
③BG-AC=CE
④S△BDG-S△CDE= S△ABC
S△ABC
其中总是成立的是________ (填序号)
①②③④
分析:连接AD,即可推出AD垂直且平分BC,根据等腰直角三角形的相关性质即可推出△ECD≌△GAD,再根据全等三角形的性质,即可推出AG=CE,DG=DE,再由AB=AC,AG=CE,可得BG-AC=BG-AB=AG,即BG-AC=CE,然后,根据所推出的结论可得S△ECD=S△GAD,S△ABC=2SADB,通过等量代换,结合图形即可推出S△BDG-S△CDE=S△BDG-S△ADG=S△ADB,即S△BDG-S△CDE= S△ABC.
S△ABC.
解答: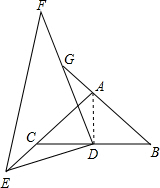 解:连接AD.
解:连接AD.
∵△ABC是等腰直角三角形,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,
∴∠ADB=∠ADC=90°,∠ACD=∠B=∠CAD=∠BAD=45°,CD=BD=AD,
∵∠EDF=90°,
∴∠ADG=∠EDC,∠ECD=∠GAD=135°,
∴在△ECD和△GAD中,
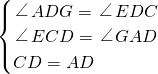
∴△ECD≌△GAD(AAS),
∴AG=CE,DG=DE,
∵AB=AC,
∴BG-AC=BG-AB=AG,
∵AG=CE,
∴BG-AC=CE,
∵△ECD≌△GAD,
∴S△ECD=S△GAD,
∵△ABC为等腰直角三角形,AD为斜边上的高,
∴S△ABC=2SADB,
∴S△BDG-S△CDE=S△BDG-S△ADG=S△ADB,
∴S△BDG-S△CDE= S△ABC,
S△ABC,
∴总上结论①②③④项均成立.
故答案为①②③④.
点评:本题主要考查等腰直角三角形的性质、全等三角形的判定及性质定理,三角形的面积公式,关键在于正确地作出辅助线,推出相关的三角形全等,认真的结合图形推出S△BDG-S△CDE=S△BDG-S△ADG=S△ADB.
分析:连接AD,即可推出AD垂直且平分BC,根据等腰直角三角形的相关性质即可推出△ECD≌△GAD,再根据全等三角形的性质,即可推出AG=CE,DG=DE,再由AB=AC,AG=CE,可得BG-AC=BG-AB=AG,即BG-AC=CE,然后,根据所推出的结论可得S△ECD=S△GAD,S△ABC=2SADB,通过等量代换,结合图形即可推出S△BDG-S△CDE=S△BDG-S△ADG=S△ADB,即S△BDG-S△CDE=
 S△ABC.
S△ABC.解答:
 解:连接AD.
解:连接AD.∵△ABC是等腰直角三角形,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,
∴∠ADB=∠ADC=90°,∠ACD=∠B=∠CAD=∠BAD=45°,CD=BD=AD,
∵∠EDF=90°,
∴∠ADG=∠EDC,∠ECD=∠GAD=135°,
∴在△ECD和△GAD中,
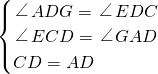
∴△ECD≌△GAD(AAS),
∴AG=CE,DG=DE,
∵AB=AC,
∴BG-AC=BG-AB=AG,
∵AG=CE,
∴BG-AC=CE,
∵△ECD≌△GAD,
∴S△ECD=S△GAD,
∵△ABC为等腰直角三角形,AD为斜边上的高,
∴S△ABC=2SADB,
∴S△BDG-S△CDE=S△BDG-S△ADG=S△ADB,
∴S△BDG-S△CDE=
 S△ABC,
S△ABC,∴总上结论①②③④项均成立.
故答案为①②③④.
点评:本题主要考查等腰直角三角形的性质、全等三角形的判定及性质定理,三角形的面积公式,关键在于正确地作出辅助线,推出相关的三角形全等,认真的结合图形推出S△BDG-S△CDE=S△BDG-S△ADG=S△ADB.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一定点,延长BP至P′,将△ABP绕点A旋转后,与△ACP′重合,如果AP=
 如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是
如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 (2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )
(2012•资阳)如图,△ABC是等腰三角形,点D是底边BC上异于BC中点的一个点,∠ADE=∠DAC,DE=AC.运用这个图(不添加辅助线)可以说明下列哪一个命题是假命题?( )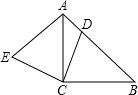 已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.
已知:如图,△ABC是等腰直角三角形,D为斜边AB上任意一点(不与A,B重合),连接CD,作EC⊥DC,且EC=DC,连接AE.