题目内容
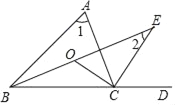
【题目】如图，已知OD=OC,添加下列四个条件中的一个，仍不能得到△ODA与△OCB全等的是（ ）
A.∠D=∠CB.OA=OBC.BD=ACD.AD=BC
【答案】D
【解析】
三角形全等条件中必须是三个元素，并且一定有一组对应边相等．在△ODA与△OCB中，已知OD=OC，公共角∠O，因此只需添加一组对应角相等或OA=OB即可判定两三角形全等．
解：已知OD=OC，公共角∠O，，
A、如添加∠D=∠C，利用ASA即可证明△ODA≌△OCB；
B、如添加OA=OB，利用SAS即可证明△ODA≌△OCB；
C、如添加BD=AC，因为OD=OC，则OA=OB，利用SAS能证明△ODA≌△OCB；
D、如添AD=BC，因为SSA，不能证明△ODA≌△OCB，所以此选项不能作为添加的条件．
故选：D．
练习册系列答案
相关题目
