题目内容
如图，在五边形ABCDE中，∠A=∠B，∠C=∠D=∠E=90°，DE=DC=4，AB=
，则五边形ABCDE的周长是
- A.
- B.
- C.
- D.
B
分析：可连接CE，作AF⊥CE，BG⊥CE于F、G，根据多边形的内角和定理和等腰直角三角形的性质即可求出AB、AE+BC，进而求出答案．
解答：
解：连接CE，作AF⊥CE，BG⊥CE于F、G，
根据五边形的内角和定理和已知条件，可得△CDE，△AEF，△BCG都是等腰直角三角形，
则CE=4，
∴FG=AB=，
∴AE+BC=3×=6，
所以五边形的周长是4+4+6+=14+．
故选B．
点评：此题主要是作辅助线，发现等腰直角三角形．注意：等腰直角三角形的斜边是直角边的倍．
分析：可连接CE，作AF⊥CE，BG⊥CE于F、G，根据多边形的内角和定理和等腰直角三角形的性质即可求出AB、AE+BC，进而求出答案．
解答：
解：连接CE，作AF⊥CE，BG⊥CE于F、G，根据五边形的内角和定理和已知条件，可得△CDE，△AEF，△BCG都是等腰直角三角形，
则CE=4
，∴FG=AB=
，∴AE+BC=3
×=6，所以五边形的周长是4+4+6+
=14+．故选B．
点评：此题主要是作辅助线，发现等腰直角三角形．注意：等腰直角三角形的斜边是直角边的
倍． 
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
7、如图，在五边形ABCDE中，BC∥AD，BD∥AE，AB∥EC．图中与△ABC面积相等的三角形有（ ）
如图，在五边形ABCDE中，∠ABC=∠AED=90°，M是CD的中点，BM=EM，求证：∠BAC=∠EAD．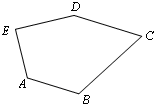
19、如图，在五边形ABCDE中，AE⊥DE，∠BAE=120°，∠BCD=60°，∠CDE-∠ABC=30°．
如图：在五边形ABCDE中，∠ABC=∠AED=90°，∠BAC=∠EAD，M是CD中点，试判断
点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上．设点P的运动时间为t（s）．