题目内容
 25、请为下面题目的说明过程加上理由.
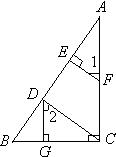
25、请为下面题目的说明过程加上理由.已知如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,试说明CD⊥AB的理由.
理由:因为DG⊥BC,AC⊥BC,(已知),
所以∠DGB=∠ACB=90°(垂直的定义).
所以DG∥AC(
同位角相等,两直线平行
),所以∠2=∠DCA,(
两直线平行,内错角相等
).因为∠1=∠2,
所以∠1′=∠DCA.
所以EF∥CD,(
同位角相等,两直线平行
).所以∠AEF=∠ADC(
两直线平行,同位角相等;
).因为EF⊥AB,所以∠AEF=90°.
所以∠ADC=90°,即CD⊥AB.
分析:根据解题过程和平行线的性质与判定填空.
解答:解:理由:∵DG⊥BC,AC⊥BC,(已知),
∴∠DGB=∠ACB=90°(垂直的定义).
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠DCA,(两直线平行,内错角相等).
∵∠1=∠2,
∴∠1=∠DCA.
∴EF∥CD,(同位角相等,两直线平行).
∴∠AEF=∠ADC(两直线平行,同位角相等).
∵EF⊥AB,
∴∠AEF=90°.
∴∠ADC=90°,即CD⊥AB.
∴∠DGB=∠ACB=90°(垂直的定义).
∴DG∥AC(同位角相等,两直线平行),
∴∠2=∠DCA,(两直线平行,内错角相等).
∵∠1=∠2,
∴∠1=∠DCA.
∴EF∥CD,(同位角相等,两直线平行).
∴∠AEF=∠ADC(两直线平行,同位角相等).
∵EF⊥AB,
∴∠AEF=90°.
∴∠ADC=90°,即CD⊥AB.
点评:本题主要考查解题的依据,需要熟练掌握平行线的性质与判定.

练习册系列答案
相关题目

 (AD+BC)利用上面的知识,完成下面题目的解答已知:直线l与抛物线M交于点A,B两点,抛物线M的对称轴为y轴,过点A,B作x轴的垂线段,垂足分别为D,C,已知A(-1,3),B(
(AD+BC)利用上面的知识,完成下面题目的解答已知:直线l与抛物线M交于点A,B两点,抛物线M的对称轴为y轴,过点A,B作x轴的垂线段,垂足分别为D,C,已知A(-1,3),B(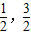 )
)