题目内容
 如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE=
如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE= .
.
(1)求 ;
;
(2)证明:直线DE是半圆O的切线.
 (1)解:连接OD,作OF⊥CD于点F.
(1)解:连接OD,作OF⊥CD于点F.∵CD=6,∴
 .
.∵
 .
.∴
 ;
;答;
 的值为
的值为 ;
;(2)证明:∵
 ,
,∴由(1)知
 ,
,∵CD∥AB,
∴∠CDO=∠DOE.
∴△DOF∽△OED,
∴∠ODE=∠OFD=90°,
∴OD⊥DE,
∴直线DE与半圆O相切.
分析:(1)连接OD,作OF⊥CD于点F,根据CD=6利用垂径定理可得DF,再利用OB+BE即可求出OE.然后即可求出
 的值;
的值;(2)由(1)知
 ,利用CD∥AB,求证△DOF∽△OED,可得∠ODE=∠OFD=90°,即可证明直线DE与半圆O相切.
,利用CD∥AB,求证△DOF∽△OED,可得∠ODE=∠OFD=90°,即可证明直线DE与半圆O相切.点评:此题主要考查切线的判定,垂径定理,相似三角形的判定与性质等知识点,解答此题的关键是作好辅助线:连接OD,作OF⊥CD于点F.这也是此题的突破点,此题有一定的拔高难度,属于中档题.

练习册系列答案
相关题目
 如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.
如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC.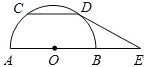 如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE=
如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE=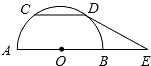 如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE=
如图所示,已知AB是半圆O的直径,弦CD∥AB,AB=10,CD=6,E是AB延长线上一点,BE=
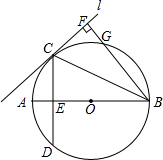 为F,BF交⊙O于C.
为F,BF交⊙O于C.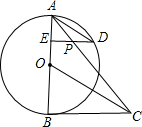 如图所示,已知AB是⊙O的直径,BC是⊙O的切线,OC平行于弦AD,过点D作DE⊥AB于点E,连接AC,与DE交于点P.问EP与PD是否相等?证明你的结论.
如图所示,已知AB是⊙O的直径,BC是⊙O的切线,OC平行于弦AD,过点D作DE⊥AB于点E,连接AC,与DE交于点P.问EP与PD是否相等?证明你的结论.