Question

如图，一被冰雪压垮的高压铁塔从A处折断，塔尖着地．经测量，折断部分AC与地面的夹角α=43°，塔身部分AB在某一时刻阳光下的影长BD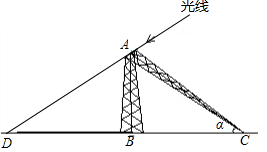=12米，而在同一时刻身高1.8米的工人的影子长为2.7米．求铁塔原来的高度（精确到0.1米）．（参考数据：sin43°=0.68，cos43°=0.73，tan43°=0.93）

Answer 1

分析：利用比例式求得AB的长，然后在Rt△ACB中求得AC的长，两者相加即可得到铁塔的高度．

解答：解：依题意，得

AB

BD

=

1.8

2.7

∴AB=

2

3

×12=8（米）       
在Rt△ACB中     
 AC=

AB

sinα

=

8

0.68

≈11.8（米）
∴8+11.8=19.8（米）      
答：铁塔原来的高度为19.8米．

点评：本题考查了解直角三角形的知识，解题的关键是正确的构造直角三角形并求解．