题目内容
已知关于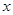 的方程
的方程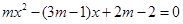 .
.
1.求证:无论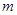 取任何实数时,方程恒有实数根;
取任何实数时,方程恒有实数根;
2.若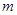 为整数,且抛物线
为整数,且抛物线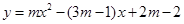 与
与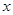 轴两交点间的距离为2,求抛物线的解析式
轴两交点间的距离为2,求抛物线的解析式
3.若直线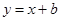 与(2) 中的抛物线没有交点,求
与(2) 中的抛物线没有交点,求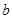 的取值范围.
的取值范围.
1.分两种情况讨论.
① 当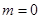 时,方程为
时,方程为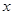
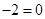
∴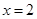 方程有实数根
-----------------------------1分
方程有实数根
-----------------------------1分
②当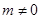 ,则一元二次方程的根的判别式
,则一元二次方程的根的判别式
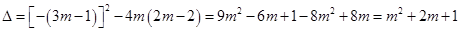
=
∴不论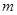 为何实数,
为何实数,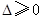 成立,
成立,
∴方程恒有实数根 -----------------------------------------3分
综合①、②,可知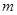 取任何实数,方程
取任何实数,方程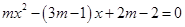 恒有实数根
恒有实数根
2.设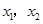 为抛物线
为抛物线 与
与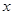 轴交点的横坐标.
轴交点的横坐标.
令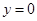 , 则
, 则 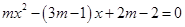
由求根公式得,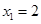 ,
,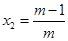 -------------------------------------5分
-------------------------------------5分
∴抛物线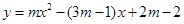 不论
不论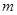 为任何不为0的实数时恒过定点
为任何不为0的实数时恒过定点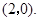 -----------------------6分
-----------------------6分
∵ 
∴ 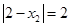
∴ 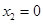 或
或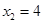 ,----------------------------------------------------------8分
,----------------------------------------------------------8分
∴ 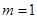 或
或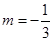 (舍去)
(舍去)
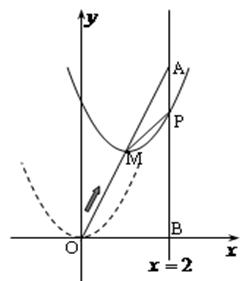
∴求抛物线解析式为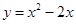 ,
----------------------------------------9分
,
----------------------------------------9分
3.由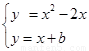 ,得
,得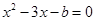
∴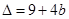 --------------------------------------10分
--------------------------------------10分
∵直线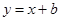 与抛物线
与抛物线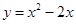 没有交点
没有交点
∴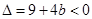
∴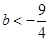 -------------------------------------11分
-------------------------------------11分
所以,当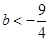 , 直线
, 直线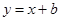 与(2)中的抛物线没有交点. --------------12分
与(2)中的抛物线没有交点. --------------12分
【解析】(1)分两种情况讨论.①当m=0时,方程为x-2=0求出方程的解x=2;②当m≠0,则得到一个一元二次方程,求出方程的根的判别式△=(m+1)2得出不论m为何实数,△≥0成立,即可得到答案;
(2)设x1,x2为抛物线y=mx2-(3m-1)x+2m-2与x轴交点的横坐标.求出方程mx2-(3m-1)x+2m-2=0的解x1=2,x2= 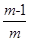 ,根据题意得出|2-x2|=2,求出x,x2=0或x2=4,进一步求出m即可;
,根据题意得出|2-x2|=2,求出x,x2=0或x2=4,进一步求出m即可;
(3)把方程组 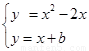 ,转化成方程x2-3x-b=0,根据题意求出△=9+4b<0,解不等式即可.
,转化成方程x2-3x-b=0,根据题意求出△=9+4b<0,解不等式即可.

| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
 的方程
的方程 .
.
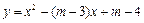 与
与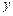 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求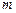 的值.
的值.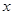 的方程
的方程
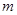 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)