题目内容
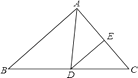
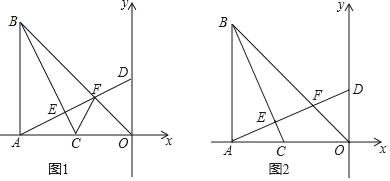
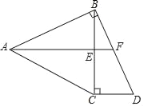
【题目】如图,在等腰△ABC中,AB=AC,过点B作BD⊥AB,过点C作CD⊥BC,两线相交于点D,AF平分∠BAC交BC于点E,交BD于点F.
(1)若∠BAC=68°,求∠DBC;
(2)求证:点F为BD中点;
(3)若AC=BD,且CD=3,求四边形ABDC的面积.
【答案】(1)∠DBC=34°;(2)见解析;(3)四边形ABDC的面积=27.
【解析】
(1)根据等腰三角形的性质得到AE⊥BC,∠BAE=![]() ∠BAC=34°,根据余角的性质得到结论;
∠BAC=34°,根据余角的性质得到结论;
(2)根据平行线等分线段定理即可得到结论;
(3)根据全等三角形的性质得到BE=CD=3,求得BC=6,根据全等三角形的性质即可得到结论.
(1)∵AB=AC,AF平分∠BAC,
∴AE⊥BC,∠BAE=![]() ∠BAC=34°,
∠BAC=34°,
∵BD⊥AB,
∴∠AEB=∠ABF=90°,
∴∠DBC=∠BAE=34°;
(2)∵CD⊥BC,AE⊥BC,
∴EF∥CD,
∵BE=CE,
∴BF=DF,
∴点F为BD中点;
(3)∵AC=BD,AB=AC,
∴AB=BD,
在△ABE与△BCD中,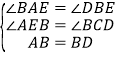 ,
,
∴△ABE≌△BCD(AAS),
∴BE=CD=3,
∴BC=6,
∴四边形ABDC的面积=3S△BCD=3×![]() ×3×6=27.
×3×6=27.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
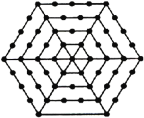
【题目】如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
(1)填写下表:
层 数 | 1 | 2 | 3 | 4 | 5 | … |
该层对应的点数 | 1 | 6 | … |
(2)写出第n层所对应的点数(n≥2).
(3)如果某一层共96个点,你知道它是第几层吗?
(4)有没有一层,它的点数为100个?
(5)写出n层的六边形点阵的总点数.