题目内容
(本题满分8分)
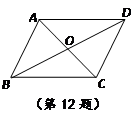
如图,四边形 是面积为4的正方形,函数
是面积为4的正方形,函数 (
( )的图象经过点
)的图象经过点 .
.

(1)求 的值;
的值;
(2)将正方形 分别沿直线
分别沿直线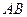 、
、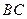 翻折,得到正方形
翻折,得到正方形 、
、 .设线段
.设线段 、
、 分别与函数
分别与函数 (
( )的图象交于点
)的图象交于点 、
、 ,求线段EF所在直线的解析式.
,求线段EF所在直线的解析式.
如图,四边形
 是面积为4的正方形,函数
是面积为4的正方形,函数 (
( )的图象经过点
)的图象经过点 .
.
(1)求
 的值;
的值;(2)将正方形
 分别沿直线
分别沿直线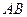 、
、 翻折,得到正方形
翻折,得到正方形 、
、 .设线段
.设线段 、
、 分别与函数
分别与函数 (
( )的图象交于点
)的图象交于点 、
、 ,求线段EF所在直线的解析式.
,求线段EF所在直线的解析式. (1)4
(2)

(1)∵四边形 是面积为4的正方形,
是面积为4的正方形,
∴ =2.
=2.
∴点 坐标为(2,2).
坐标为(2,2).
∴ =2×2=4.
=2×2=4.
(2)∵正方形 、
、 由正方形
由正方形 翻折所得,
翻折所得,
∴ =4,
=4,
∴点 横坐标为4,点
横坐标为4,点 纵坐标为4.
纵坐标为4.
∵点 、
、 在函数y=的图像上,
在函数y=的图像上,
∴当 时,
时, ,即
,即 .
.
当 时,
时, ,即
,即 .
.
设直线 解析式为
解析式为 ,将
,将 、
、 两点坐标代入,
两点坐标代入,
得
∴ .
.
∴直线 解析式为
解析式为 .
.
 是面积为4的正方形,
是面积为4的正方形,∴
 =2.
=2.∴点
 坐标为(2,2).
坐标为(2,2).∴
 =2×2=4.
=2×2=4.(2)∵正方形
 、
、 由正方形
由正方形 翻折所得,
翻折所得,∴
 =4,
=4,∴点
 横坐标为4,点
横坐标为4,点 纵坐标为4.
纵坐标为4.∵点
 、
、 在函数y=的图像上,
在函数y=的图像上,∴当
 时,
时, ,即
,即 .
.当
 时,
时, ,即
,即 .
.设直线
 解析式为
解析式为 ,将
,将 、
、 两点坐标代入,
两点坐标代入,得

∴
 .
. ∴直线
 解析式为
解析式为 .
.
练习册系列答案
相关题目
 = DC=1,BD平分∠ABC,BD⊥CD.
= DC=1,BD平分∠ABC,BD⊥CD.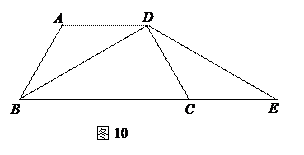
 E=CD,说明△DBE是等腰三角形
E=CD,说明△DBE是等腰三角形 BC,E是垂足,如果∠B=50°,那么∠D、
BC,E是垂足,如果∠B=50°,那么∠D、 
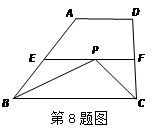

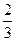 ,BF=3米,BC=1米,CD=6米.求:
,BF=3米,BC=1米,CD=6米.求: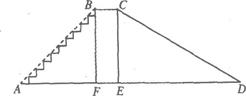
 ,有以下四个条件:①
,有以下四个条件:①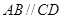 ;②
;②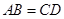 ;③
;③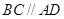 ;④
;④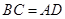 .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形