题目内容
 (1)计算:
(1)计算:
(2)计算:(8x4+4x3-16x2)÷(-2x)2
(3)如图,四边形ABCD是正方形,△ADE旋转后能与△ABF重合.
①旋转中心是哪个点?
②旋转了多少度?
③连接EF,则△AEF是什么三角形?说明理由.
解:(1)3× -
- +
+ +
+ ,
,
=3× -10+10-1,
-10+10-1,
= -1,
-1,
= ;
;
(2)(8x4+4x3-16x2)÷(-2x)2,
=(8x4+4x3-16x2)÷4x2,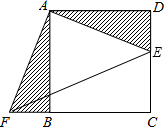
=8x4÷4x2+4x3÷4x2-16x2÷4x2,
=2x2+x-4;
(3)①由图可知,旋转中心是点A;
②∵四边形ABCD是正方形,
∴∠BAD=90°,
∴旋转了90°;
③△AEF是等腰直角三角形.
理由如下:∵△ADE旋转后能与△ABF重合,
∴AE=AF,∠BAF=∠DAE,
∴∠EAF=∠BAF+∠BAE=∠DAE+∠BAE=∠BAD=90°,
∴△AEF是等腰直角三角形.
分析:(1)根据算术平方根的定义,立方根的定义化简,然后进行计算即可得解;
(2)先根据积的乘方的性质计算,再根据多项式除以单项式的运算法则进行计算即可得解;
(3)①根据图形可知,公共点A为旋转中心;
②对应边AB、AD之间的夹角即为旋转角;
③根据旋转的性质可得AE=AF,再求出∠EAF=∠BAD=90°,然后判断出△AEF是等腰直角三角形.
点评:本题考查了旋转的性质,正方形的性质,等腰直角三角形的判定,实数的运算,多项式除以单项式,是基础题,熟记运算法则与定义是解题的关键.
 -
- +
+ +
+ ,
,=3×
 -10+10-1,
-10+10-1,=
 -1,
-1,=
 ;
;(2)(8x4+4x3-16x2)÷(-2x)2,
=(8x4+4x3-16x2)÷4x2,

=8x4÷4x2+4x3÷4x2-16x2÷4x2,
=2x2+x-4;
(3)①由图可知,旋转中心是点A;
②∵四边形ABCD是正方形,
∴∠BAD=90°,
∴旋转了90°;
③△AEF是等腰直角三角形.
理由如下:∵△ADE旋转后能与△ABF重合,
∴AE=AF,∠BAF=∠DAE,
∴∠EAF=∠BAF+∠BAE=∠DAE+∠BAE=∠BAD=90°,
∴△AEF是等腰直角三角形.
分析:(1)根据算术平方根的定义,立方根的定义化简,然后进行计算即可得解;
(2)先根据积的乘方的性质计算,再根据多项式除以单项式的运算法则进行计算即可得解;
(3)①根据图形可知,公共点A为旋转中心;
②对应边AB、AD之间的夹角即为旋转角;
③根据旋转的性质可得AE=AF,再求出∠EAF=∠BAD=90°,然后判断出△AEF是等腰直角三角形.
点评:本题考查了旋转的性质,正方形的性质,等腰直角三角形的判定,实数的运算,多项式除以单项式,是基础题,熟记运算法则与定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
随机抽取某城市30天的空气质量状况统计如下:
其中,ω≤50时,空气质量为优;50<ω≤100时,空气质量为良;100<ω≤150时,空气质量为轻微污染.
(1)请分别算出这30天里空气质量为优、良、轻微污染所占的百分比;
(2)请用扇形统计图表示(1)的计算结果;
(3)估计该城市一年(以365天计)中有多少天空气质量达到良以上.
| 污染指数(ω) | 40 | 70 | 90 | 110 | 120 | 140 |
| 天数(t) | 3 | 5 | 10 | 7 | 4 | 1 |
(1)请分别算出这30天里空气质量为优、良、轻微污染所占的百分比;
(2)请用扇形统计图表示(1)的计算结果;
(3)估计该城市一年(以365天计)中有多少天空气质量达到良以上.



