题目内容
我们已经学习了一次函数和反比例函数,在这过程中我们积累了丰富的探究函数 图象及其性质的经验.请你自主探索函数y=ax3(a≠0,a为常数)性质.
图象及其性质的经验.请你自主探索函数y=ax3(a≠0,a为常数)性质.(1)请你在所给的平面直角坐标系中画出函数y=
| 1 |
| 8 |
(2)观察(1)中图象,写出函数y=
| 1 |
| 8 |
(3)请你写出函数y=ax3(a≠0,a为常数)的两条性质.
分析:先在函数图象上取几个点并且求出对应的y的值,在坐标系内描出这些对应的点,画出函数图象,根据函数的图象写出对应的函数的性质即可.
解答:解:(1)

(2)由(1)中函数y=
x3的图象可知此图象具有以下性质:
①函数的图象在一、三象限,在每一象限内y随x的增大而增大;
②函数的图象关于原点对称.
(3)由(2)的结论可知,函数y=ax3(a≠0,a为常数)具有以下性质:
①当a>0时,函数的图象在一、三象限,当a<0时,函数的图象在二、四象限;
②函数的图象关于原点对称.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ||||||||
| y | -
|
-1 | -
|
0 |
|
1 |
|

(2)由(1)中函数y=
| 1 |
| 8 |
①函数的图象在一、三象限,在每一象限内y随x的增大而增大;
②函数的图象关于原点对称.
(3)由(2)的结论可知,函数y=ax3(a≠0,a为常数)具有以下性质:
①当a>0时,函数的图象在一、三象限,当a<0时,函数的图象在二、四象限;
②函数的图象关于原点对称.
点评:此题属于探索性题目,解答此题的关键是利用描点法画出函数的图象,再由函数图象的性质进行解答.

练习册系列答案
相关题目
 图象及其性质的经验.请你自主探索函数y=ax3(a≠0,a为常数)性质.
图象及其性质的经验.请你自主探索函数y=ax3(a≠0,a为常数)性质.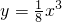 的图象.
的图象.