Question

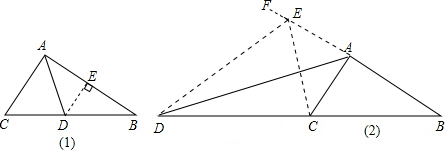
已知，在△ABC中，∠ACB=2∠B．
（1）如图1，当AD为∠BAC的角平分线时，求证：AB=AC+CD；
（2）如图2，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，对你的猜想加以证明．

Answer 1

分析：（1）在AB上取一点E，使得AE=AC，连接DE，证明△ACD≌△AED，得出CD=DE，及证明△EDB为等腰三角形，得出DE=BE，得出AB=AC+CD；
（2）在AB的延长线AF上取一点E，使得AE=AC，连接DE．证明△ACD≌△AED，DE=BE，BE=CD，得出结论．

解答：明：在AB上取一点E，使得AE=AC，连接DE
在△ACD和△AED中，

AC=AE ∠CAD=∠EAD AD=AD

，
∴△ACD≌△AED（SAS），
∴∠C=∠AED，CD=DE，
，又∵∠C=2∠B，
∴∠AED=2∠B，
又∵∠AED=∠B+∠EDB，
∴DE=BE，
∴BE=CD，
∴AB=AC+CD；

（2）AB=CD-AC
证明：在BA的延长线AF上取一点E，使得AE=AC，连接DE
在△ACD和△AED中，

AC=AE ∠CAD=∠EAD AD=AD

，
∴△ACD≌△AED（SAS），
∴∠ACD=∠AED，CD=DE，
∴∠ACB=∠FED，
又∵∠ACB=2∠B，
∴∠FAD=2∠B，
又∵∠FED=∠B+∠EDB，
∴∠EDB=∠B，
∴DE=BE，
∴BE=CD，
∴AB=CD-AC．

点评：本题考查了全等三角形的判定、三角形的角平分线的性质及三角形内外角的关系；正确作出辅助线是解答本题的关键，证明线段的和差问题往往是通过全等来证明的．